На эти три вопроса ответ содержится в изложенных выше трех теоремах подобия (разделы 2, 4).
Нахождение параметров эмпирических зависимостей методом наименьших квадратов состоит в том, что по экспериментальным точкам необходимо провести кривую (не ломаную), которая проходила бы как можно ближе к истинной функциональной зависимости y = f(t). Теория вероятности показывает, что наилучшим приближением будет такая кривая (или прямая) линия, для которой сумма квадратов расстояний по вертикали от точек до кривой будет минимальной. Этот метод и называется методом наименьших квадратов. Сущность этого метода состоит в следующем.
Предположим, что искомая зависимость выражается функцией
y = f(t, А1 , А2,…, Аm ), где А1 , А2,…, Аm - параметры. Значения этих параметров определяются так, чтобы точки yi располагались по обе стороны кривой y = f(t) как можно ближе к последней, т.е. чтобы сумма квадратов отклонений измеренных значений yi от функции y = f(t) была бы наименьшей. Это соответствует предположению, что разброс точек yi относительно кривой y = f(t) подчиняется закону нормального распределения. Мерой этого разброса является дисперсия s2 или ее приближенное выражение – средний квадрат отклонений:
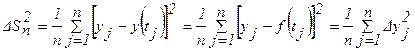 . (5.1)
. (5.1)
Известно, что функция f (А) принимает минимальное значение при А = Аmin , если ее первая производная 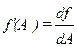 равна нулю, а вторая производная
равна нулю, а вторая производная 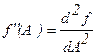 положительна. Для функции многих переменных эти условия заменяются требованием, чтобы частные производные, т.е. производные по параметру Аi, удовлетворяли вышеупомянутым условиям, причем все остальные параметры Аj (j ¹i) при вычислении производных считаются постоянными.
положительна. Для функции многих переменных эти условия заменяются требованием, чтобы частные производные, т.е. производные по параметру Аi, удовлетворяли вышеупомянутым условиям, причем все остальные параметры Аj (j ¹i) при вычислении производных считаются постоянными.
Таким образом, из условия минимума f (А) получаем систему уравнений для определения наилучших значений параметров:
 (5.2)
(5.2)
(i=1, 2,…, m; m < n)
При задании зависимости y = f(t, А1 , А2,…,Аn) в виде полинома:
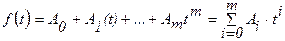 , (m<n-1,) (5.3)
, (m<n-1,) (5.3)
уравнения (5.2) принимают вид
 , (i = 0,1,…,m); m<n-1. (5.4)
, (i = 0,1,…,m); m<n-1. (5.4)
Решение этих систем линейных уравнений позволяет однозначно определить коэффициенты Аi разложения y = f(t).
Изложенный способ обобщается и на некоторые случаи нелинейных зависимостей f(t, А1 , А2,…,Аm ) от параметров, например, для
 (5.5).
(5.5).
В этом случае целесообразно искать не минимум суммы квадратов отклонений функций  , а минимум суммы квадратов отклонений логарифмов этих же функций (рисунок 5.1).
, а минимум суммы квадратов отклонений логарифмов этих же функций (рисунок 5.1).
Найдем параметры квадратичной зависимости вида у (t) = а + bt + ct2.

Рисунок 5.1 - Кривая y=y(t) , построенная по значениям (ti, yi) методом
наименьших квадратов
Потребуем, чтобы сумма квадратов отклонений имела минимальное значение
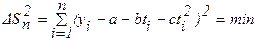 . (5.6)
. (5.6)
Дифференцируя это соотношение по a, b и c, получим:
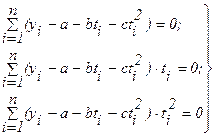 (5.7)
(5.7)
т.е. :
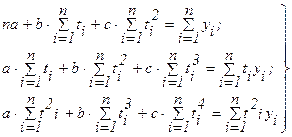 (5.8)
(5.8)
Из этой системы можно определить значения параметров a, b, c.
Если один из параметров зависимости, например, b равен нулю, то система уравнений для этого случая может быть получена из первого и третьего уравнений, полагая в них b = 0.
При изучении конкретного процесса обычно всегда ставится задача получить при этом данные и для расчета других процессов, подобных изучаемому. Для того, чтобы результат отдельных опытов можно было распространить на все подобные ему процессы, обработка результатов опытов должна проводиться в критериях подобия.
В процессе вычисления критериев подобия при обобщении опытных данных необходимо учитывать изменения физических свойств рабочих сред, участвующих в процессе теплообмена жидкости или газа. Один из путей учета состоит в определении физических свойств с помощью введения так называемой определяющей температуры, по которой определяются значения параметров, входящих в критерии подобия. Довольно распространенным является выбор в качестве определяющей средней температуры  где tw – температура стенки, tf – температура жидкости. Однако следует помнить, что универсальной температуры, выбором которой во всех случаях автоматически учитывалась бы зависимость теплообмена от изменения физических свойств с температурой не существует. За определяющую температуру целесообразно принимать такую, которая в расчетах задана или легко может быть определена, а влияние изменения физических свойств теплоносителя учитывать путем введения дополнительной поправки (множителя) в обобщенные критериальные зависимости.
где tw – температура стенки, tf – температура жидкости. Однако следует помнить, что универсальной температуры, выбором которой во всех случаях автоматически учитывалась бы зависимость теплообмена от изменения физических свойств с температурой не существует. За определяющую температуру целесообразно принимать такую, которая в расчетах задана или легко может быть определена, а влияние изменения физических свойств теплоносителя учитывать путем введения дополнительной поправки (множителя) в обобщенные критериальные зависимости.
При обобщении опытных данных важным также является вопрос о выборе определяющего размера. Целесообразно выбирать тот размер, которым определяется развитие процесса. При этом обобщенные зависимости для однотипных, но геометрически не подобных систем оказываются близкими или даже одинаковыми, что представляет удобство для практических расчетов.
Предположим, что в процессе теплообмена была получена функциональная зависимость:
Nu = f (Re, Pr) (5.9)
По данным измерений подсчитываются значения критериев Re и Pr и соответствующие им значения Nu.
Зависимость между критериями подобия (аргументов в количестве 2 –4 критерия) обычно представляется в виде степенных функций, например:
Nu = с × Ren × Prm , (5.10)
где с, n, m являются постоянными безразмерными числами.
Такого рода зависимости являются чисто эмпирическими (опытными). Они применимы лишь в тех пределах изменения аргумента, в которых подтверждены опытом. Экстраполяция этих зависимостей на большие или меньшие значения определяющих критериев, строго говоря, недопустима.
Предположим, что критерий Nu зависит только от критерия Re (или, что опыты проводились с теплоносителем, критерий Прандтля которого является постоянной величиной, не зависящей от температуры). В этом случае
Nu = с × Ren . (5.11)
Логарифмируя последнее уравнение, получим:
ln Nu = ln с + ln Re (5.12)
Обозначая ln Nu = Y, ln Re = X, ln с = A, можно написать:
Y = A + nX. (5.13)
Последнее уравнение является уравнением прямой линии.
Показатель степени n представляет собой тангенс угла наклона прямой к оси абсцисс (рисунок 5.2). Значение n можно определить с помощью графического представления опытных данных в координатах ln Nu = f(ln Re), однако для этого необходимо выбрать одинаковый масштаб величин на осях координат.
В последнем случае
n = tg j = 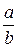 . (5.14)
. (5.14)
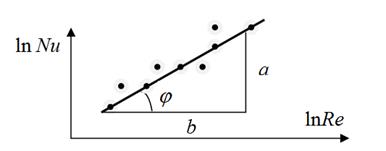
Рисунок 5.2 - К установлению зависимости вида Nu = с × Ren
Постоянная с определяется из уравнения  , которому удовлетворяет любая точка прямой.
, которому удовлетворяет любая точка прямой.
В случае, если искомая величина Nu является функцией двух аргументов, например, Nu = f (Re, Pr), на графике получается семейство прямых; второй аргумент берется в качестве параметра (рисунок 5.3).
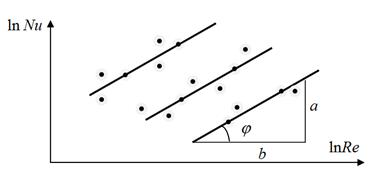
Рисунок 5.3 К установлению зависимости вида Nu – с× Ren Pr m
Тогда по одной из прямых определяют показатель при критерии Рейнольдса, а затем опытные данные представляют на графике в виде зависимости 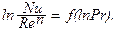
Из последнего графика определяют показатель степени т при критерии Прандтля, а затем по уравнению 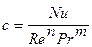 определяют значение коэффициента с. Аналогичным путем можно устанавливать зависимости и с большим числом критериев подобия.
определяют значение коэффициента с. Аналогичным путем можно устанавливать зависимости и с большим числом критериев подобия.
В последнее время все шире используется полуэмпирический метод получения критериальных уравнений. Зависимость между критериями представляется в виде функции, получаемой предварительно с точностью до постоянных из аналитического рассмотрения задачи. Постоянные уточняются с помощью опытных данных. Такой путь получения критериальных уравнений является предпочтительным по сравнениюс эмпирическим.
Рассмотрим пути нахождения параметров критериальной зависимости в виде степенной функции:
 . (5.15)
. (5.15)
Логарифмируя (5.14), получим:
 . (5.16)
. (5.16)
Из условия минимума суммы:
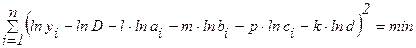 . (5.17)
. (5.17)
после дифференцирования по  , получаем уравнения:
, получаем уравнения:
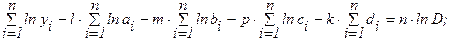


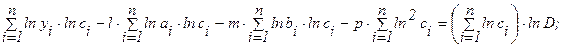
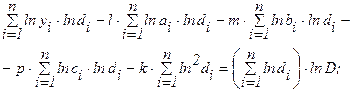 (5.18)
(5.18)
Обозначая:
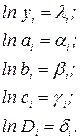
получим систему 5-ти линейных уравнений с 5-ю неизвестными l, m, p, n, d, которая может быть решена аналитически.
Дата добавления: 2015-12-26; просмотров: 1693;
