Алгоритм решения задач на пересечение поверхностей

Пересечением поверхностей называется кривая, точки которой принадлежат одновременно обеим поверхностям.

В начертательной геометрии линию пересечения двух поверхностей находят с помощью приема, которым называется способом вспомогательных секущих поверхностей.

Этот способ заключается в следующем,

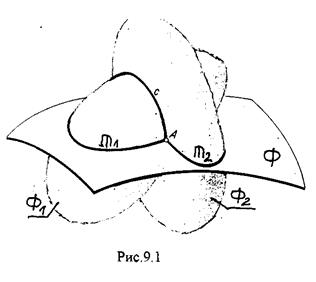
Пусть надо построить линию пересечения двух поверхностей Ф₁ и Ф₂. Выбирается третья поверхность Ф. Затем находится линия пересечения поверхностей Ф и Ф₁, Ф и Ф₂. Вид и расположение поверхности Ф относительно данных поверхностей должны быть выбраны так, чтобы в пересечении получились простые по форме линии (прямая или окружность), чтобы проекции этих линий было легко построить. Последовательность действий можно представить алгоритмом:

1)Выбор вспомогательной секущей поверхности Ф;

2)ФÇФ₁= m₁, ФÇФ2 = m_2;

3)m₁Çm₂ = M, m₁Çm2 = N...

Полученные точки М, N и т.д. принадлежат обеим поверхностям одновременно, следовательно, принадлежат искомой линии пересечения.

9.2. Метод секущих плоскостей

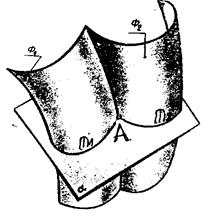
При построении линии пересечения двух поверхностей методом секущих плоскостей в качестве вспомогательной секу-щей поверхности выбирается плоскость. Вспомогательная плоскость выбирается таким образом, чтобы она пересекала данные поверхности по прямым или окружностям. Алгоритм в этом случае будет следующим:

2) Находим линии пересечения Ф₁Ça =m₁, Ф₂Ça=m₂;

3) m₁Çm₂ = A, m₁Çm₂ = В, … и т. д. (Рис.9.2.)

Применение метода секущих плоскостей при

Решении задач

На рис.9.3. даны конус и полусфера.

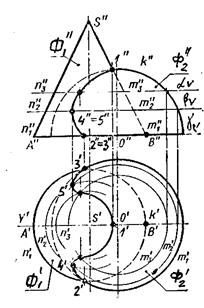В данном случае в качестве вспомогательных секущих плоскостей необходимо выбрать плоскости, параллельные горизонтальной плоскости проекций, так как такие плоскости пересекают конус и полусферу по окружностям.

Так как основания обеих поверхностей лежат в одной плоскости, то точки пересечения окружностей 2 и 3 также являются общими точками для данных поверхностей.

Точки 1,2,3 являются опорными, точка 1 - самая высокая, точки 2, 3- самые низкие. Теперь обе поверхности пересечем плоскостью a, расположенной ниже точки 1 и выше точек 2 и 3. Эта плоскость a пересечет обе поверхности по окружностям n₂ и m₂ найдем точки пересечения полученных окружностей n₂Çm₂ = 4, :n₂ Ç m₂ = 5.

Точки 4,5 принадлежат линии пересечения конуса и полусферы. Повторив это действие, необходимое число раз, построим линию пересечения данных поверхностей.