Определитель поверхности, каркас поверхности
Поверхность можно представить как общую часть двух смежных областей пространства. В начертательной геометрии поверхность определяется как совокупность последовательных положений линии, перемещающейся в пространстве по определенному закону. Такой способ образования поверхности называется кинематическим. Линия, перемещающаяся в пространстве, называется образующей. Образующая может быть прямой линией или кривой. Она может иметь постоянную форму или менять ее в процессе перемещения. Закон перемещения в пространстве образующей удобно задавать в виде совокупности неподвижных линий. Их называют направляющими. Процесс образования поверхности показан на рис.8.1.
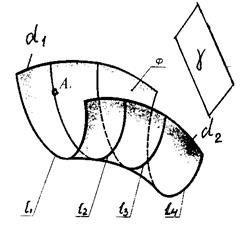 Образующей является кривая 1. Закон перемещения задан двумя направляющими d1, d2 и плоскостью g. Обра-зующая 1 скользит по направ-ляющим d1 и d2, оставаясь параллельной плоскости g, Точка А, принадлежащая поверхности принадлежит 12.
Образующей является кривая 1. Закон перемещения задан двумя направляющими d1, d2 и плоскостью g. Обра-зующая 1 скользит по направ-ляющим d1 и d2, оставаясь параллельной плоскости g, Точка А, принадлежащая поверхности принадлежит 12.
 Поверхность определена, если можно однозначно решить, принадлежит точка пространства данной поверхности или нет. Совокупность условий, задающих поверх-ность в пространстве и на чертеже, называется опре-делителем поверхности.
Поверхность определена, если можно однозначно решить, принадлежит точка пространства данной поверхности или нет. Совокупность условий, задающих поверх-ность в пространстве и на чертеже, называется опре-делителем поверхности.
Определитель состоит из двух частей геометрической и алгоритмической. Геометрическая часть определителя это перечень геометрических элементов, участвующих в образовании поверхности. Алгоритмическая часть - указывает на взаимосвязь между элементами.
Одна и та же поверхность может быть образована разными способами, поэтому может иметь различные определители. Например, поверхность прямого кругового цилиндра можно представить:
а) как результат вращения прямой 1 при ее вращении вокруг оси i С (1, i); [вращение 1 вокруг i];
б) как результат вращения кривой k, точки которой равноудалены от оси i, вокруг оси i. С (k., i); [ вращение k вокруг i];
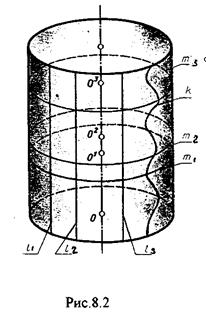 в) как результат поступательного перемещения окружности m. При этом центр окружности 0 перемещается по оси i, а ее плоскость a остается перпендикулярной к оси i C(m.i); [ поступательное, 0 Î i, 1Ìa ^ i]. Из множества определителей выбирают наиболее простой. В данном случае - вариант (а).
в) как результат поступательного перемещения окружности m. При этом центр окружности 0 перемещается по оси i, а ее плоскость a остается перпендикулярной к оси i C(m.i); [ поступательное, 0 Î i, 1Ìa ^ i]. Из множества определителей выбирают наиболее простой. В данном случае - вариант (а).
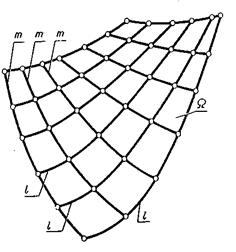
 Упорядоченное множество точек или линий, принадлежащих поверхности называется ее каркасом (рис.8.3). Каркас поверхности может быть точечным или линейным. Линейным каркасом называется множество линий имеющих единый закон образования и связанных между собой определенной зависимостью. Эта зависимость называется параметром каркаса. Если параметр каркаса непрерывная функция, каркас называется непрерывным, т.е. через любую точку поверхности проходит одна линия.
Упорядоченное множество точек или линий, принадлежащих поверхности называется ее каркасом (рис.8.3). Каркас поверхности может быть точечным или линейным. Линейным каркасом называется множество линий имеющих единый закон образования и связанных между собой определенной зависимостью. Эта зависимость называется параметром каркаса. Если параметр каркаса непрерывная функция, каркас называется непрерывным, т.е. через любую точку поверхности проходит одна линия.
Каркасом задают сложные поверхности технических объектов, таких как обшивки самолетов, автомобилей, судов, лопатки турбин, насосов. Каркасные поверхности задают на чертеже проекциями элементов каркаса (рис.8.4.).
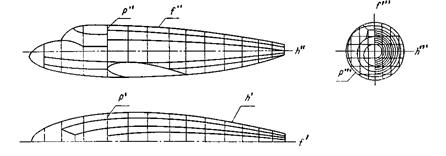 Каркас таких поверхностей называется дискретным. В этом случае положение точки, не принадлежащей линии каркаса можно определить только приближенно.
Каркас таких поверхностей называется дискретным. В этом случае положение точки, не принадлежащей линии каркаса можно определить только приближенно.
|
| |
|
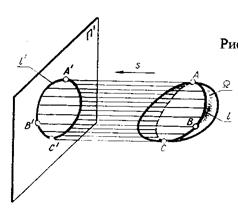 Задание поверхности проекциями определителя не всегда обеспечивает нагляд-ность, что затрудняет чтение чертежа. Для придания чертежу поверхности нагляд-ности его дополняют очер-ковыми линиями очерком поверхности (при ортого-нальном проецировании) называют след на плос-кости проекции проецирующей цилиндрической поверхность, которая огибает данную поверхность. Рис.8.5.
Задание поверхности проекциями определителя не всегда обеспечивает нагляд-ность, что затрудняет чтение чертежа. Для придания чертежу поверхности нагляд-ности его дополняют очер-ковыми линиями очерком поверхности (при ортого-нальном проецировании) называют след на плос-кости проекции проецирующей цилиндрической поверхность, которая огибает данную поверхность. Рис.8.5.
Дата добавления: 2016-01-20; просмотров: 1288;
