Поверхности вращения. Поверхности вращения создаются при вращении прямолинейной или криволинейной образующей m вокруг неподвижной оси 1
Поверхности вращения создаются при вращении прямолинейной или криволинейной образующей m вокруг неподвижной оси 1. (Рис.8.13.а.)
Благодаря простоте формирования этих поверхностей они получили широкое применение в технике. Геометрическая часть определителя поверхности вращения состоит всего из двух линий: образующей m и оси i.
Алгоритмическая часть определителя включает так же две операции:
1) на образующей m выделяют ряд точек А, В, С ... К.
2) каждую точку вращают вокруг оси i.
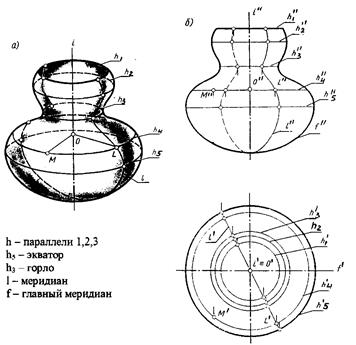 Так создается каркас поверхности, состоящий из множества окружностей, плоскости которых распологаются перпендикулярно оси i. Эти окружности называются параллелями. Наименьшая параллель называется горлом, наиболъшая экватором. Линии, полученные в сечении поверхности плоскостями, проходящими через ось, называются меридианами. Плоскость, перпендикулярная оси вращения пересекает поверхность по окружности - параллели.
Так создается каркас поверхности, состоящий из множества окружностей, плоскости которых распологаются перпендикулярно оси i. Эти окружности называются параллелями. Наименьшая параллель называется горлом, наиболъшая экватором. Линии, полученные в сечении поверхности плоскостями, проходящими через ось, называются меридианами. Плоскость, перпендикулярная оси вращения пересекает поверхность по окружности - параллели.
|
На чертеже ось поверхности вращения располагают перпендикулярноодной из плоскостей проекций. Так на рис.8.13. ось i ^ H.
На плоскость Н в этом случае проецируются все параллели, а на плоскость V - два меридиана, которые определяют фронтальный очерк. Меридиан, расположенный в плоскости, параллельной V называют главным. Для того чтобы найти горизонтальную проекцию произвольной точки М, принадлежащей поверхности вращения, проводят через М² фронтальную проекцию параллели. Затем, простроив проекцию этой параллели на плоскости Н, определяют М¢.
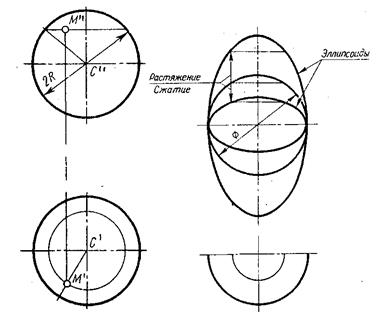
1. Сфера. Образуется вращением окружности вокруг оси, проходящей через центр сферы. При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть образованы и при вращении эллипса вокруг одной из его осей. Если осью вращения является большая ось эллипса, эллипсоид называется вытянутым, а если меньшая то сжатым (Рис.8.14.)
|
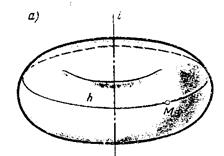
2. Тор. Поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр, Рис.8.21.
| |
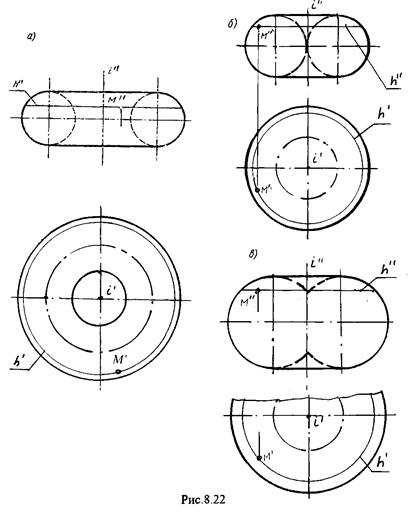
 Различают;
Различают;
а) открытый тор (рис.8.16,а), б) замкнутый (рис.8.16.б.),
в) самопересекающейся
(рис.8.16,в.).
 Отсеки тора, обра-зованные вращением дуги окружности называются глобоидами. Рис.8.17.
Отсеки тора, обра-зованные вращением дуги окружности называются глобоидами. Рис.8.17.
| |||
|
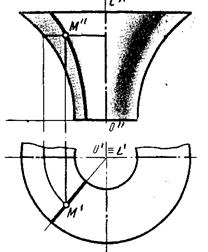
Рис.8.17.
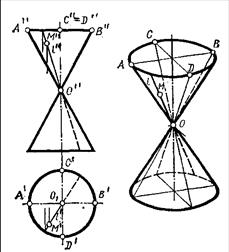
При вращении вокруг оси прямой линии образуется цилиндрическая поверхность вращения (образующая параллельна оси вращения) и коническая поверхность вращения (образующая пересекает ось вращения) (рис. 8.18., 8.19.)
|
|

9. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Дата добавления: 2016-01-20; просмотров: 1576;
