Метод эксцентрических сфер

Рассмотрим пересечение конуса и тора (рис.9.6.). Ось конуса параллельна V, а ось вращения тора j перпендикулярна V. Ocь конуса i и круговая ось тора q лежат в общей плоскости симметрии d, параллельной плоскости V. По отношению к плоскости V плоскость d является главной меридиональной плоскостью Поэтому плоскость d пересекает конус по образующим, а тор - по двум дугам окружности. Оба сечения проецируются на плоскости V очерковыми линиями проекций тора и конуса. Очерковые линии пересекаются в точках 1² и 2², которые являются проекциями точек 1 и 2, принадлежащими линии l пересечения рассматриваемых поверхностей. Эти точки являются опорными. Проведем через ось тора j плоскость Г. Плоскость Г пересечет тор по окружности р, а его круговую ось - в точке С. Окружность р проецируется на плоскость V отрезком р² , равным ее диаметру.

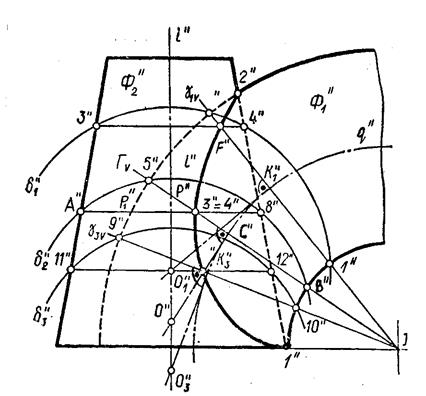
Определим точки 3 и 4 пересечения окружности р с поверхностью конуса. Для этого заключим окружность р в вспомогательную сферу. Центр сферы должен находиться на оси конуса. Только в этом случае сфера пересечет конус по окружности, по тому проекцию центра сферы О² найдем как точку пересечения касательной С²О² к центровой окружности тора с осью конуса. Радиус сферы равен R. Сфера пересечет конус по окружности р_ь Окружность кольца р и окружность p₁ конуса располагаются на одной сфере и, следовательно, пересекается в точках 3 и 4, принадлежащих искомой линии пересечения конуса и тора.

Другие точки, принадлежащие пересечению конуса с тором, строятся по только что рассмотренному алгоритму с помощью других радиальных плоскостей.