Пересечение поверхности плоскостью
Конические сечения
(сечения прямого кругового конуса плоскостью)
Если секущая плоскость не параллельна ни одной из образующих конуса, то в сечении получается эллипс.
Если секущая плоскость параллельна одной образующей, то в сечении будет парабола.
Если пересечь конус плоскостью, параллельной двум его образующим, то в сечении получится гипербола.
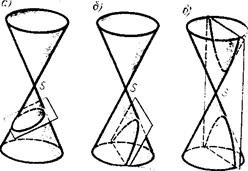Признаки, по которым можно определить вид кривой, даны на рис.9.15.
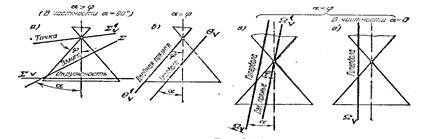
1) a>j - эллипс
1) a=j - парабола
2) a<j – гипербола
a = 0 гипербола (рис.9.15).
|
|
Рассмотрим построение линии пересечения конуса вращения фронтально - проецирующей плоскостью Q (рис.9.17.). В сечении получим эллипс. Так как плоскость Q перпендикулярна плоскости V, то эллипс на фронтальную плоскость проекций проецируется в отрезок К²Р². Этот отрезок является большой осью эллипса, а малая ось эллипса проецируется в середину отрезка К²Р² - в точку Е².
|
Для построения горизонтальной проекции эллипса необходимо на заданном отрезке выбрать несколько точек и провести через них образующие или параллели конуса. Затем построить горизонтальные проекции образующих и параллелей. Используя принадлежность точек соответствующим образующим или параллелям, построить горизонтальную проекцию эллипса.
Используя те же принципы, можно построить проекции линии пересечения в остальных случаях.
Конус пересечен горизонтально- проецирующей плоскостью S. В сечении получим гиперболу. Так как горизонтальная проекция плоскости S совпадает с горизонтальным следом, то горизонтальной проекцией гиперболы является отрезок В¢А¢.
Чтобы построить фронтальную проекцию гиперболы на данном отрезке необходимо выбрать несколько точек и построить их фронтальные проекции. Для этого на отрезке А¢В¢ выберем несколько точек, через которые проведем образующие или параллели конуса. Построив фронтальные проекции выбранных образующих или параллелей конуса, построим фронтальные проекции выбранных точек (например: F и G).
Обязательно надо построить самую высокую точку С. Она лежит в плоскости T^S. На горизонтальной проекции имеем С¢=Sh ÇTH.
Чтобы построить С², надо построить фронтальную проекцию образующей SK. Это будет прямая S²К². На ней получим точку С². Аналогичным способом строим точку D. Берем D¢ на образующей S¢N¢, строим S¢¢N¢¢, затем точку D¢¢. Эту точку нужно строить обязательно, так как в этой точке происходит переход с видимой на невидимую сторону поверхности (рис.9.18.),
|
Сечение сферы
Дата добавления: 2016-01-20; просмотров: 1422;