Построение линии пересечения поверхностей, когда
Одна проецирующая
Поверхности цилиндра и призмы иногда могут располагаться по отношению к плоскостям проекций таким образом, что образующие цилиндра или боковые ребра и боковые грани призмы окажутся перпендикулярными какой — то плоскости проекций. Такое положение поверхности называется проецирующим. Проекцией такой поверхности является окружность, если это цилиндр, или многоугольник, если это призма. В таком случае построение линии пересечения поверхностей упрощается.
Рассмотрим пример: необходимо построить линию пересечения двух цилиндров, один из которых расположен вертикально. Образующие такого цилиндра перпендикулярны плоскости Н. Второй полуцилиндр расположен таким образом, что образующие этого полуцилиндра перпендикулярны плоскости W. (Рис.9.10.)
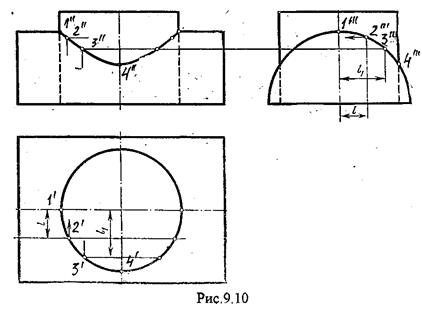 При таком расположении цилиндров горизонтальная проекция линии пересечения совпадает с окружностью - горизонтальной проекции цилиндра с вертикальной осью, а профильная проекция линии пересечения совпадает с полуокружностью профильной проекцией полуцилиндра с горизонтальной осью. Это выполняется потому что вертикальный цилиндр занимает горизонтально - проецирующее положение, а полуцилиндр - профильно проецирующее положение. Построение фронтальной проекции линии пересечения осуществляется по правилам построения третьей проекции точки, если известны две ее другие проекции.
При таком расположении цилиндров горизонтальная проекция линии пересечения совпадает с окружностью - горизонтальной проекции цилиндра с вертикальной осью, а профильная проекция линии пересечения совпадает с полуокружностью профильной проекцией полуцилиндра с горизонтальной осью. Это выполняется потому что вертикальный цилиндр занимает горизонтально - проецирующее положение, а полуцилиндр - профильно проецирующее положение. Построение фронтальной проекции линии пересечения осуществляется по правилам построения третьей проекции точки, если известны две ее другие проекции.
Рассмотрим еще один пример: построим линию пересечения конуса с цилиндром. Цилиндр занимает горизонтально – проецирующее положение, следовательно, горизонтальной проекцией цилиндра является окружность, горизонтальная проекция линии пересечения цилиндра и конуса совпадает с горизонтальной проекцией цилиндра, т.е. окружностью. Чтобы построить фронтальную проекцию линии пересечения необходимо выбрать точки на окружности. Сначала выбираем характерные точки линии пресечения. Это точки 1,2,3,4,5,6, Точки 1,6 являются крайними. Отмечают их горизонтальные проекции 1¢,6¢. Так как это точки лини пересечения поверхностей, то они одновременно принадлежат цилиндру и конусу. Точки 1,6 принадлежат окружности основания конуса.
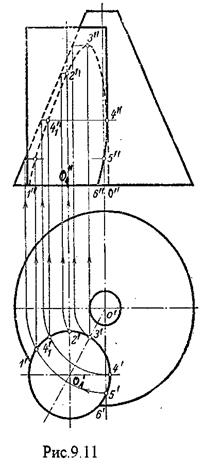 Используя эту принад-лежность, находим фронтальные проекции точек 1²6². Точка 3 так же является характерной, так как она принадлежит плоскости a, проходящей через оси вращения данных поверхностей. В этой плоскости находятся самая вы-сокая и самая низкая точка линии пересечения. Точка 3 находится на окружности, принадлежащей конусу. Эта окружность на горизонтальную плоскость проекции проецируется в натуральную величину а на фрон-тальную плоскость - в отрезок. Выбрав горизонтальную проек-цию 3¢, проводим окружность, находим фронтальную проекцию этой окружности, на ней находим точку 3². (Нахождение фрон-тальной проекции окружности видно из рис.9.11.). Точка 2 - самая дальняя, 4 - самая правая, 5 - самая близкая. Построив харак-терные точки, проекцию линии пересечения построить еще сложно, можно выбрать промежуточные (например: 41), и осуществить точно такие построения.
Используя эту принад-лежность, находим фронтальные проекции точек 1²6². Точка 3 так же является характерной, так как она принадлежит плоскости a, проходящей через оси вращения данных поверхностей. В этой плоскости находятся самая вы-сокая и самая низкая точка линии пересечения. Точка 3 находится на окружности, принадлежащей конусу. Эта окружность на горизонтальную плоскость проекции проецируется в натуральную величину а на фрон-тальную плоскость - в отрезок. Выбрав горизонтальную проек-цию 3¢, проводим окружность, находим фронтальную проекцию этой окружности, на ней находим точку 3². (Нахождение фрон-тальной проекции окружности видно из рис.9.11.). Точка 2 - самая дальняя, 4 - самая правая, 5 - самая близкая. Построив харак-терные точки, проекцию линии пересечения построить еще сложно, можно выбрать промежуточные (например: 41), и осуществить точно такие построения.
В других случаях построение осуществляется аналогично. Одна проекция линии совпадает с проекцией проецирующей поверхности, а для построения f второй проекции линии пересечения надо использовать принадлежность линии второй поверхности.
Чтобы построить точку, принадлежащую поверхности, надо через данную точку провести линию, принадлежащую данной поверхности. Это может быть образующие, или окружности в зависимости от поверхности.
|
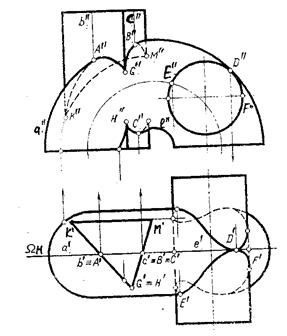
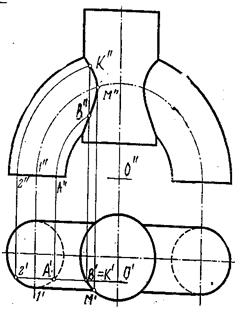
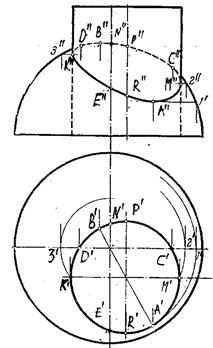 Рис.9.12.
Рис.9.12.
|
Дата добавления: 2016-01-20; просмотров: 3521;
