Метод концентрических сфер

В этом случае в качестве вспомогательных секущих поверхностей выбираются концентрические сферы.

Применение этого метода основано на следующем свойстве: Две поверхности вращения, имеющие общую ось (соосные поверхности), пересекаются по окружностям. Действительно, кривая m образует поверхность вращения с осью вращения i, кривая n образует вторую поверхность вращения с той же осью i. Если mÇn = А, то точка А опишет окружность, которая является общей для обеих поверхностей, следовательно, является линией их пересечения. (Рис.9.4.)

Если ось i перпендикулярна плоскости Н, то окружность, описываемая точкой А, проецируется на фронтальную плоскость проекций в отрезок, а на горизонтальную плоскость в окружность.

Из сказанного можно сделать следующие выводы:

1. Для того, чтобы вспомогательная секущая сфера пересекала по окружностям две заданные поверхности вращения, центр сферы должен лежать в точке пересечения осей этих поверхностей.

2. Если оси заданных поверхностей вращения параллельны плоскости проекций, то окружности пересечения вспомогательной секущей сферы с этими поверхностями проецируется на эту плоскость в отрезки.

Теперь можно сформулировать условия, необходимые для применения метода концентрических секущих сфер:

1. Данные поверхности должны быть поверхностями вращения;

2. Оси вращении данных поверхностей должны пересекаться;

3. Плоскость, проходящая через оси вращения данных поверхностей, должна быть параллельна какой - нибудь плоскости проекций.

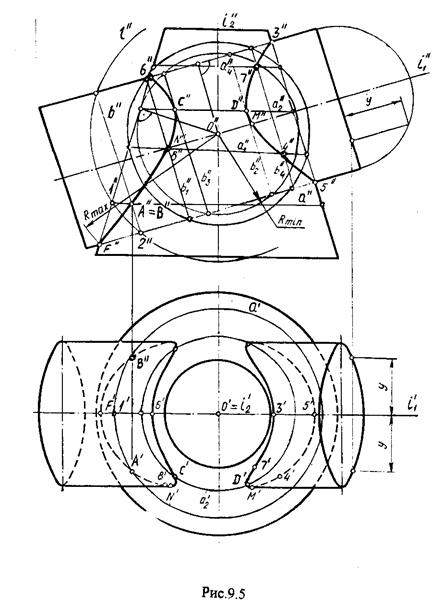
Построение линии пересечения начинается с построения опорных точек (Рис.9.5.). Чтобы построить опорные точки надо построить сферу минимального радиуса. Сфера минимального радиуса вписана в одну поверхность и пересекает вторую.

Общие точки С и Д окружности касания с конусом и окружности пересечения с цилиндром являются опорными точками. К опорным точкам относятся также точки пересечения фронтальных очерков данных поверхностей. Отрезок O²F² где f² наиболее удаленная от точки О² точка пересечения очерков данных поверхностей определяет сферу максимального радиуса.

Для построения промежуточных точек необходимо выбрать сферу радиуса R, где R_min< R< R_max.

1. Для этого из центра О²= i²₂ Ç i²₁ нужно провести окружность произвольного радиуса, являющейся проекцией сферы.

2. Построим линию пересечения сферы с конусом. Это будет окружность, которая на фронтальную плоскость проекций проецируется в отрезок. Затем построим линию пересечения сферы с цилиндром. Это тоже окружность, которая тоже проецируется в отрезок, точки пересечения А и В данных окружностей являются точками пересечения цилиндра и конуса. Для построения других промежуточных точек нужно из точки О² описать ряд концентрических окружностей и проделать те же построения.