Линейчатые поверхности
Поверхность называется линейчатой, если она образована движением прямой линии по какому - нибудь закону. Закон ее движения обычно задается направляющими. В общем случае линейчатая поверхность может быть получена движением прямой линии по трем направляющим.
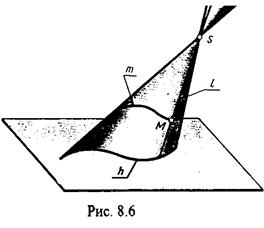
Коническая поверхность образуется перемещением прямой 1 (образующей) по кривой направляющей m и, проходящей через фиксированную точку S (вершину). a (1,m,S); (liÇm, SÎli),(Рис.8.6.) Точка М, принадлежащая поверхности конуса, принадлежит образующей 1.
 Цилиндрическая поверхность b (рис.8.9.) образуется перемеще-нием прямой образую-щей 1 по кривой направляющей m. При этом образующие параллель-ны заданному направле-нию s Цилиндрическую поверхность можно рассматривать как частный случай кони-ческой поверхности с бесконечно удаленной вершиной s.
Цилиндрическая поверхность b (рис.8.9.) образуется перемеще-нием прямой образую-щей 1 по кривой направляющей m. При этом образующие параллель-ны заданному направле-нию s Цилиндрическую поверхность можно рассматривать как частный случай кони-ческой поверхности с бесконечно удаленной вершиной s.
b (1, m, s); (li Ç m, li // s ).
Точка М, принадлежащая цилиндру, принадлежит образующей 1.
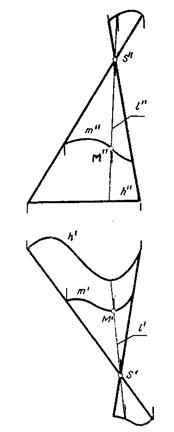
На комплексном чертеже коническая и цилиндрическая поверхности могут быть заданы проекциями направляющей m и вершины S в случае конической поверхности (рис.8.7.) или проекциями направляющей m и направления s образующей в случае цилиндрической поверхности (рис.8.10). Обычно при задании конической или цилиндрической поверхности в качестве направляющей выбирается, какая - нибудь линия уровня, например горизонталь h.
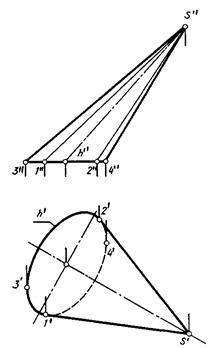
Для увеличения наглядности изображения конической и цилиндрической поверхностей на комп-лексном чертеже, помимо элементов, определяющих эти поверхности., дополнительно строят их очерки.
|
| |||
| |||

|
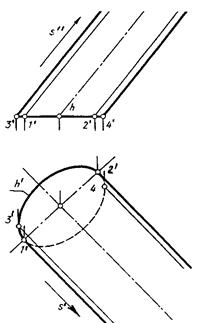
 При этом горизонтальные проекции точек 1 и 2 являются точками касания к проекции hi направляющей h очерковых образующих, а проекции 3 и 4 являются точками касания к h1 линий связи. Этими очерковыми образующими определяются на плоскостях проекций области, внутри которых могут находиться проекции точек данных поверхностей, а также производится разграничение проекций поверхностей на видимую и невидимую части на каждой из плоскостей проекций.
При этом горизонтальные проекции точек 1 и 2 являются точками касания к проекции hi направляющей h очерковых образующих, а проекции 3 и 4 являются точками касания к h1 линий связи. Этими очерковыми образующими определяются на плоскостях проекций области, внутри которых могут находиться проекции точек данных поверхностей, а также производится разграничение проекций поверхностей на видимую и невидимую части на каждой из плоскостей проекций.
|
|
|
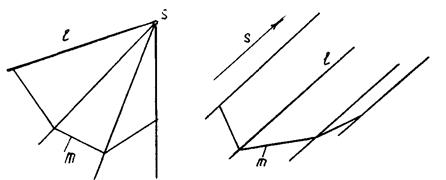 Если направляющей является ломаная линия, то получим частные случаи конической и цилиндрической поверхности - пирамидальную и призматическую поверхности.
Если направляющей является ломаная линия, то получим частные случаи конической и цилиндрической поверхности - пирамидальную и призматическую поверхности.
Дата добавления: 2016-01-20; просмотров: 1188;
