АГЕНТЫ, РЕШАЮЩИЕ ЗАДАЧИ
Необходимость для интеллектуальных агентов принимать на себя обязанность достичь цели и стремиться к ее выполнению, максимизировать свои показатели производительности покажем на конкретном примере поведения некоторого туриста во время его отпуска в городе Арад (Румыния). Комплекс намерений туриста может включать: предпочтительное посещение отдельных городов и посёлков, осмотр достопримечательностей, посещение музеев, усовершенствование знания иностранного языка, улучшение загара и т. д. Относительная сложность задачи принятия решения определяется необходимостью учета множества компромиссов и внимательного чтения путеводителей, стремлением туриста к достижению цели – своевременно попасть в Бухарест. В общем случае туристу требуется также оценивать последствия, связанные с изменениями в расписании полета, продолжительностью переезда между терминалами аэропорта, возможными переездами из одного аэропорта в другой и т. п.
Первым шагом в решении задачи является формулировка целис учетом текущей ситуации и показателей производительности агента.
Формулировка задачипредставляет собой процесс определения того, какие действия и состояния следует рассматривать с учетом некоторой цели. В нашем примере состояния, рассматриваемые агентом, соответствуют его пребыванию в конкретном городе. Агент поставил перед собой цель доехать на автомобиле до Бухареста. Из города Арада в Бухарест ведут три дороги: через Сибиу, Тимишоару и Зеринд. Агент, не очень знакомый с географией Румынии, не знает, какое из его возможных действий является наилучшим. Все, что он может сделать, – это выбрать одно из указанных направлений случайным образом. При наличии карты Румынии агент получает возможность исследовать различные последовательности действий, которые приводят к состояниям с известной стоимостью, и выбирать из них наилучшую последовательность.
Любой алгоритм поиска принимает в качестве входных данных некоторую задачу и вырабатывает решение в форме последовательности действий. После выполнения этого решения агент формулирует новую цель. Вначале рассмотрим процесс формулировки задачи, а затем различные алгоритмы поиска. Задача формально определяется с помощью следующих четырех компонентов:
· Начальное состояние, в котором агент приступает к работе. Например, начальное состояние нашего агента в Румынии может быть описано как пребывание в Араде. Каждое последующее состояние представляется местонахождением и, возможно, текущим временем.
· Функция определения преемника – описание возможных действий, доступных агенту. В функции следования каждое действие представляет собой одно из допустимых действий в состоянии x, а каждый преемник представляет собой состояние, которое может быть достигнуто из состояния x путем применения этого действия. Для нашей задачи проезда
по Румынии множество всех состояний, достижимых из начального состояния, выглядит следующим образом (рис. 26).
Маршрут в движения определяется последовательностью действий в пространстве состояний.
· Проверка цели позволяет определить, является ли данное конкретное состояние целевым. Цель агента в рассматриваемом примере является одноэлементным множеством – прибыть в Бухарест. Иногда цель задается в виде абстрактного свойства, а не в виде перечисленного множества состояний.
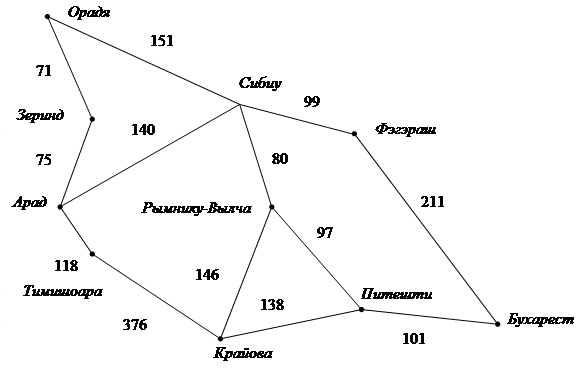
Рис. 26. Упрощенная дорожная карта части Румынии
Например, в шахматах цель состоит в достижении состояния, называемого «матом», в котором король атакован и не может уклониться от удара.
· Функция стоимости пути назначает числовое значение стоимости каждого пути. Стоимости этапов на рис. 26 показаны в виде дорожных расстояний.
Собранные вместе описанные выше элементы представляют собой единую структуру входных данных для алгоритма решения задачи, т. е. определения пути от начального состояния до целевого. Качество решения измеряется функцией стоимости пути, а оптимальное решение имеет наименьшую стоимость пути среди всех прочих решений.
ПРИМЕРЫ ЗАДАЧ
Приведем примеры решения упрощенных задач, предназначенных для иллюстрации или проверки различных методов решения, и реальных задач, которые действительно требуются людям и не имеют, как правило, единого приемлемого для всех описания.
Примеры упрощенных задач
Задача игры в восемь. Вариант, который показан на рис. 27, состоит из доски, размеченной на 9 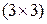 квадратов одинаковых размеров с восемью пронумерованными фишками и одним пустым участком. Фишка, смежная с пустым участком, может быть передвинута на этот участок. Требуется достичь целевого состояния, изображенного на рис. 27, б (правая сторона).
квадратов одинаковых размеров с восемью пронумерованными фишками и одним пустым участком. Фишка, смежная с пустым участком, может быть передвинута на этот участок. Требуется достичь целевого состояния, изображенного на рис. 27, б (правая сторона).
Стандартная формулировка этой задачи является следующей.
· Состояние определяется местонахождением каждой из восьми фишек и пустого участка на одном из девяти квадратов.
· Начальное состояние может быть любое, однако любая заданная цель может быть достигнута точно из половины возможных начальных состояний. Теоретически показано, что в задаче игры в восемь состояния подразделяются на два непересекающихся множества, при этом ни одно состояние из первого множества не может быть преобразовано в состояние из второго множества, даже с применением сколь угодно большого количества ходов.
· Функция определения преемника формирует допустимые состояния, которые являются результатом попыток осуществления теоретически возможных четырех ходов (Left, Right, Up или Down).
· Проверка цели позволяет определить, соответствует ли данное состояние целевой конфигурации, показанной на рис. 27.
· Стоимость пути. Если стоимость каждого этапа выбрана равной 1, стоимость пути определяется количеством этапов в пути.
Общий класс задач, к которому относятся задачи со скользящими фишками, является NP-полным и часто используется в искусственном интеллекте для проверки новых алгоритмов поиска (NP-класс, сокращение от Nondeterministic Polynomial). Это класс недетерминированных полиномиальных задач характеризуется алгоритмами, позволяющими выдвинуть гипотезу о возможном решении, а затем проверить правильность этой гипотезы с помощью полиномиальных затрат времени. Одни экземпляры NP-полных задач являются сложными, а другие простыми. Задача игры в восемь имеет 9!/2 = 181 440 состояний и легко решается. Игра в пятнадцать (на доске 4´4) имеет около 1,3 триллиона состояний, и случайно выбранные варианты можно решить оптимальным образом за несколько миллисекунд с помощью наилучших алгоритмов поиска.
Задача с восемью ферзями на шахматной доске является часто используемой экспериментальной задачей для алгоритмов поиска (рис. 28). Она состоит в размещении восьми ферзей на шахматной доске таким образом, чтобы никто из них не нападал друг на друга. Для этой задачи применяются формулировки двух основных типов. В первой формулировке предусматривается использование операторов, которые дополняют описание состояния, начиная с пустого состояния; каждое следующее действие дополняет к этому состоянию еще одного ферзя. Формулировка полного состояния предполагает первоначальную установку на доску всех восьми ферзей и их дальнейшее перемещение. При этом, если состоянием является любое расположение ферзей на доске в количестве от 0 до 8, требуется проверить » 3´1014 возможных последовательностей. В лучшей формулировке запрещается помещать ферзя на любую клетку, которая уже атакована. Для состояний с расположениями n ферзей 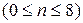 при установке по одному ферзю в каждой из находящихся слева n вертикалей таким образом, чтобы он не был атакован каким-либо другим ферзем, пространство состояний задачи сокращается с 3´1014 до 2057 и поиск решений значительно упрощается.
при установке по одному ферзю в каждой из находящихся слева n вертикалей таким образом, чтобы он не был атакован каким-либо другим ферзем, пространство состояний задачи сокращается с 3´1014 до 2057 и поиск решений значительно упрощается.
| Ф | |||||||
| Ф | |||||||
| Ф | |||||||
| Ф | |||||||
| Ф | |||||||
| Ф | |||||||
| Ф | |||||||
| Ф |
Рис. 28. Почти готовое решение задачи с восемью ферзями
(поиск окончательного решения оставлен для студентов)
Примеры реальных задач
Задачи поиска маршрута в терминах заданных местонахождений и переходов между ними характерны для самых различных приложений.
С ними приходится иметь дело в геологоразведке, при проведении военных операций, при планировании авиапутешествий, маршрутизации
в компьютерных сетях и др. Качественные решения задач поиска маршрута должны предусматривать планы действий в непредвиденных ситуациях, которые нарушают первоначальный план, требуют страховочного резервирования билетов альтернативных рейсов и дополнительных расходов.
Задача компоновки СБИС следует за этапом логического проектирования и обычно подразделяется на две части: компоновка ячеек и маршрутизация каналов. Задача компоновки требует позиционирования миллионов компонентов и соединений на микросхеме для минимизации площади, схемных задержек, паразитных емкостей и максимизации выхода готовой продукции. При компоновке ячеек простейшие компоненты схемы группируются по ячейкам, каждая из которых выполняет некоторую известную функцию. Каждую ячейку, имеющую постоянную форму (размеры и площадь) и требующую создания определенного количества соединений с другими ячейками, необходимо распределить на микросхеме таким образом, чтобы оставалось место для прокладки соединительных проводов между ячейками. Задачи маршрутизации каналов – поиск конкретного маршрута для каждого проводника через зазоры между ячейками, чрезвычайно сложные, но затраты на их решение, безусловно, оправдываются.
В задачах автоматического упорядочения сборкисложных объектов роботом цель состоит в определении последовательности, в которой должны собираться детали некоторого объекта. Одним из дорогостоящих этапов решения задачи упорядочения сборки является формирование допустимых преемников – некоторого этапа последовательности поиска, тесно связанного с задачей навигации робота. По возможности должна предотвращаться необходимость поиска во всем пространстве состояний, за исключением незначительной его части. Выбор неправильной последовательности исключает в дальнейшем нахождение способа добавления некоторой детали к этой последовательности без отмены определенной части уже выполненной работы.
В настоящее время выросла потребность в создании программных роботов для осуществления эффективного поиска необходимой информации в интернете. Для разрабатываемых в искусственном интеллекте методов поиска – это хорошее приложение, поскольку интернет легко представить концептуально в виде графа, состоящего из узлов (страниц), соединенных с помощью ссылок.
ПОИСК РЕШЕНИЙ
Рассмотрим решение сформулированных определенным образом задач методами поиска, в которых используются явно заданное дерево поиска, создаваемое с помощью начального состояния, и функции определения преемника, которые совместно задают пространство состояний. Вместо дерева поиска может применяться граф поиска, если одно и то же состояние может достигаться многими путями.
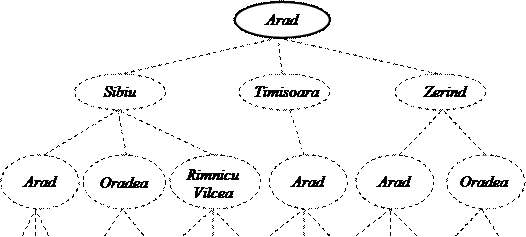
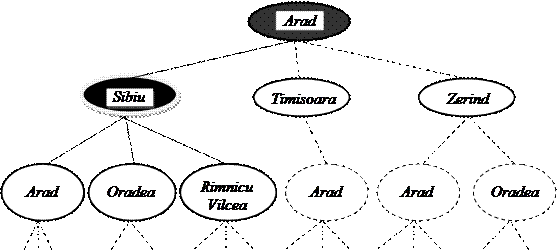
Порядок развертывания состояний определяется стратегией поиска. На рис. 29 показаны некоторые расширения дерева поиска, предназначенного для определения маршрута от города Арада до Бухареста. Первый этап состоит в проверкетого, является ли целевым начальное состояние (in Arad), соответствующее корню дерева поиска – поисковому узлу. Поскольку оно таковым не является, развертываниетекущего состояния приводит к формированию его преемника – нового множества состояний: (In Sibiu), (In Timisoara) и (In Zerind).
Суть дальнейшего поиска состоит в определении того, какой из этих трех вариантов следует рассматривать дальше. Пока проверяется один вариант, другие откладываются в сторону на тот случай, когда первый вариант не приводит к решению. Если первоначально выбран город Сибиу, проверяется на соответствие данного выбора целевому состоянию (не соответствует), после этого развертывают узел Sibiu и получают новые состояния: (In Arad), (In Fagaras), (In Oradea) и (In Rimnicu Vilcea). Необходимо снова и снова выбирать, проверять и развертывать узлы до тех пор, пока не найдется решение или не останется больше состояний, которые можно было бы развернуть.
Различие между состояниями и узлами заключается в следующем. Состояние соответствует конфигурации пространства, а узлы представляют собой структуры данных, применяемых при построении дерева поиска. Структура данных узла может включать в себя:
· состояние,соответствующее данному узлу в общем пространстве состояний;
· родительский узел;
· действие, которое было применено к родительскому узлу для формирования данного;
· стоимость пути от начального состояния до данного узла;
· глубину – количество этапов пути от первоначального состояния до данного узла.
12.4. ПРОИЗВОДИТЕЛЬНОСТЬ, ВРЕМЕННАЯ И
ПРОСТРАНСТВЕННАЯ СЛОЖНОСТЬ
АЛГОРИТМА ПОИСКА РЕШЕНИЯ ЗАДАЧИ
Производительность алгоритма решения задачи принято оценивать с помощью следующих четырех показателей:
· Полнота. Гарантирует ли алгоритм обнаружение решения, если оно имеется.
· Оптимальность. Гарантирует ли данная стратегия нахождение оптимального решения в соответствии с выбранным критерием? Обычно оцениваются стоимость, в частности, время поиска и стоимость решения.
· Временная сложность. Время нахождения решения при данном алгоритме.
· Пространственная сложность. Необходимый объем памяти для осуществления поиска.
а
б
Рис. 29. Частично развернутые деревья поиска, предназначенные для определения маршрута от города Арада до Бухареста (Развернутый узел затемнен; узлы, которые были сформированы, но еще не развернуты, выделены полужирным контуром; узлы, которые еще не были сформированы, обозначены тонкими штриховыми линиями)
а – начальное состояние; б – после развертывания узлов Arad и Sibiu
Временную сложность часто принято измерять в терминах количества узлов, вырабатываемых в процессе поиска. Пространственную сложность – в терминах максимального количества узлов, хранимых в памяти. Стоимость поиска маршрута от города Арад до Бухареста представляет собой количество времени, затраченного на этот поиск, а стоимость решения выражает общую длину пути в километрах. Поэтому для вычисления суммарной стоимости необходимо учитывать километры и миллисекунды.
| <== предыдущая лекция | | | следующая лекция ==> |
| КОМБИНИРОВАНИЕ ПРЕДСТАВЛЕНИЙ | | | ПОИСК ПО КРИТЕРИЮ СТОИМОСТИ |
Дата добавления: 2016-01-20; просмотров: 3450;
