КОМБИНИРОВАНИЕ ПРЕДСТАВЛЕНИЙ

Метод сведения задачи к подзадачам полезен для представления ее глобальных аспектов, в то время как при решении более специфических задач предпочтительнее методы, использующие пространство состояний, переписывание цепочек и перечисление. Когда применяется иерархическая структура решения, не обязательно используются одинаковые представления при решении основной задачи и всех ее подзадач. Лучше всего это можно продемонстрировать при рассмотрении проблем, затрагивающих широкие области. В качестве примера можно привести проблему, упомянутую Джоном Кеннеди в его речи по случаю избрания на пост президента США: как восстановить престиж США в мире? Эта проблема включает решение ряда подзадач, таких как активизацию программы гражданских свобод, повышение эффективности вооруженных сил и освоение космоса, в том числе и посылку человека на Луну. Далее исследование Луны требовало конструирования специальных космических кораблей. Создание космического корабля в свою очередь предполагает решение ряда инженерно-технологических и математических задач, для которых используются либо перечисление, либо переписывание цепочек.

При использовании различных представлений для решения сложных проблем вычислительные методы могут порождать так много пробных решений, что, несмотря на значительное быстродействие ЭВМ, проверить каждое из них не хватит времени. Поскольку задача обработки данных становится слишком громоздкой, правильное решение можно и не найти. Сложные по машинным стандартам задачи могут оказаться очень простыми для людей. С другой стороны, в ситуациях, когда люди не способны определить правильное решение вообще, они обычно ограничивают поиск пространством допустимых решений. Этот способ состоит в использовании планов и аналогий.

Планирование соответствуетмашинно-ориентированному понятию об иерархических отношениях между задачами и подзадачами, поэтому план определяют как решение совокупности ограниченного круга задач, каждая из которых содержит лишь некоторые основные характеристики исходной. В представлении на основе планов вырабатывается совокупность подзадач, имеющих, как ожидается, решения. Эта идея проще всего иллюстрируется задачей о «путешествующем профессоре». Предположим, профессор из Гродненского университета желает посетить коллегу из Белорусского государственного университета (город Минск). Эту задачу можно решить последовательностью действий, включающих поездки на поезде, междугороднем автобусе, автомобиле, такси и даже ходьбу. Такое путешествие сначала будет планироваться на уровне вокзалов, в предположении, что локальные транспортные проблемы будут как-то решаться по мере возникновения.

В отличие от используемого при решении задач представления на основе планов, формальное описание аналогий намного труднее. Если обратиться к представлению, основанному на сведении задачи к подзадачам при условии, что на некотором этапе выделено множество «ИЛИ подзадач», необходимо выделить и попробовать решить самую легкую из них. Во многих случаях, однако, человек не может оценить сложность решения задачи, пока не попробует. Предположим, известен способ представления и решения подзадач, аналогичных (возможно, не полная аналогия) рассматриваемой исходной задаче. Тогда в рамках такого представления следует решить все подзадачи или выделить те из них, которые можно решить, и воспользоваться полученной информацией, чтобы попытаться решить их в первоначальном представлении.

Представлениями, основанными на аналогии, в исследованиях по искусственному интеллекту часто сопровождаются решения задач из планиметрии. Формально планиметрия представляет собой аксиоматическую систему, в которой определены правильно построенные выражения на точно сформулированных правилах, в основном опирающихся на свойства конгруэнтных треугольников. Для иллюстрации метода рассмотрим пример решения следующей задачи: доказать, что диагонали параллелограмма в точке пересечения делятся пополам (рис. 25).

Дано: фигура 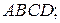параллельные стороны 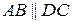и

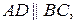
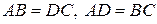; диагонал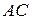и и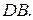

Доказать: 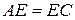и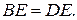

Ограничимся доказательством только одного утверждения: АЕ = ЕС. Это равенство имеет место, если отрезки АЕ и ЕС принадлежат соответствующим конгруэнтным треугольникам. Отрезок АЕ принадлежит треугольникам АЕВ и АЕD, а отрезок ЕС – треугольникам ЕСВ и ЕСD. Из рис. 25 видно, что «графически равными» являются только следующие пары треугольников:

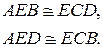(94)

Следовательно, в список подзадач, которые будут решаться программой, необходимо включать только подзадачи, соответствующие этим парам.

Рис. 25. Задача о параллелограмме

Использование аналогий в программах решения задач сопряжено с определенными трудностями, обусловленными тем, что любая неточность в аналогиях может привести к необоснованным выводам.