Глава 11. РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ РАЗЛИЧНЫХ ПРЕДСТАВЛЕНИЙ
В искусственном интеллекте о наличии задачи говорят в случаях, когда внешние воздействия окружающей среды на различные объекты и процессы отличаются от допустимого уровня, соответствующего их нормальному функционированию. Решение должно сопровождаться некоторым процессом выбора подходящих действий и разработкой соответствующей программы, осуществляющей такой выбор [1]. Когда такие действия осуществляются вслепую, то это решением задач не считается.
Человек не решает непосредственно задач, как они есть, а занимается поиском, представления их. Важность этой характерной особенности становится очевидной при анализе процесса создания программ, предназначенных для решения задач. Такие программы работают не с реальным физическим миром, а с его символьным представлением в предположении, что существует соответствие между символами и операциями над ними в машине, с одной стороны, и состояниями внешнего мира и действиями над ними, с другой. Фактически всю прикладную математику можно рассматривать подобным образом.
В тех случаях, когда физический мир и действия в нем представляются с использованием чисел и операций над ними, решается численная задача, а результат решения переводится на физический язык. Иногда такой перевод не очевиден. Например, рассмотрим задачу нахождения оптимального маршрута школьного автобуса. При определении «наилучшего маршрута» приходится во взаимосвязи решать проблемы выбора приемлемых максимального и среднего времени школьников в пути, количества и стоимости используемых для перевозки автобусов. В этом примере можно установить отдельные переменные, но во многих «реальных жизненных» ситуациях трудно оценить значения решающих переменных.
Для любого представления существенно определить, достаточно ли точно оно моделирует реальность. Важен также вопрос о полезности представления с точки зрения удобства работы с ним, что предполагает наличие вполне определенных сведений, как о собственно задаче, так и о тех, кто должен ее решать. Например, при работе с логарифмической линейкой пользователь знает, что для умножения полезно аналоговое представление чисел, а при работе на счетах он предпочтет цифровое представление. Различаются представления, которые используются при решении задач человеком и машиной.
Наличие связи между представлениями и процедурой решений проиллюстрируем задачей, связанной с изучением распространения информации о новейших достижениях в науке среди ученых. В рассматриваемом примере ученый делает открытие и извещает о нем через свои личные контакты, на научных конференциях и семинарах. Необходимо оценить, насколько быстро распространяются новости об этом открытии. В приведенном ниже списочном представлении ученых конкретизируются лица, с которыми каждый из них беседует:
1. Джонс Смит, Томас
2. Смит Джонс, Браун, Грин
3. Томас Джонс, Бейкер, Браун
4. Грин Смит, Браун
5. Браун Смит, Грин, Томас
6. Бейкер Томас, Уайт
7. Уайт Бейкер
8. Беннет Мейзон, Джеймс
9. Мейзон Беннет
10. Джеймс Беннет
Об открытии Джонса на первой встрече от автора узнают Смит и Томас, которые в свою очередь на второй встрече расскажут об этом открытии своим друзьям, так что после второй встречи список осведомленных будет включать пять человек: Джонсона, Смита, Томсона, Грина и Бейкера. На каждом этапе добавляются новые имена, но уже после трех встреч такие имена будут отсутствовать. Данный процесс определяет путь и необходимое число шагов для распространения новости.
Представление рассмотренного примера в виде графа (рис. 22) по сравнению со списочной моделью имеет определенные преимущества благодаря своей наглядности. Из графа сразу видно, что общество ученых распадается на две группы, не связанные между собой: нет возможности передать сообщение от Джонса к Беннету, Мейзону и Джеймсу; дальше всех от достижимых для Джонса лиц находится Уайт (расстояние по графу равно 3 дугам). Если бы граф был значительно сложнее, например, из-за большего количества имен, пришлось бы вернуться к списочному представлению. Люди могут справляться с задачами достаточно большой сложности, но в данном случае нельзя недооценивать трудности из-за человеческих ошибок при подсчетах.

Матричное представление применяется для решения задач с помощью машины, но людям пользоваться им затруднительно. Определим через 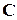 матрицу, элементы которой
матрицу, элементы которой 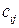 равны 1 тогда и только тогда, когда ученый i общается с ученым j, и 0 в противном случае; считаем
равны 1 тогда и только тогда, когда ученый i общается с ученым j, и 0 в противном случае; считаем 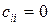 . На рис. 23 показана матрица, соответствующая графу на рис. 22.
. На рис. 23 показана матрица, соответствующая графу на рис. 22.
Рис. 23. Матрица связности для сети,
изображенной на рис. 22
Коэффициент 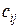 матрицы обозначает число путей (не более одного) от ученого i к ученому j, имеющих длину 1. Для определения количества путей
матрицы обозначает число путей (не более одного) от ученого i к ученому j, имеющих длину 1. Для определения количества путей 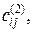 ведущих от ученого i к ученому j и имеющих длину 2, необходимо подсчитать число путей длиной 1, ведущих от ученого i к ученому k, и число таких путей от ученого k к ученому j:
ведущих от ученого i к ученому j и имеющих длину 2, необходимо подсчитать число путей длиной 1, ведущих от ученого i к ученому k, и число таких путей от ученого k к ученому j:
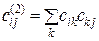 . (87)
. (87)
Чтобы найти число путей 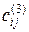 от лица
от лица 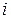 к лицу
к лицу 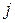 длиной 3, для всех
длиной 3, для всех 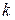 определяется число путей длиной 2, ведущих от лица
определяется число путей длиной 2, ведущих от лица 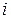 к лицу
к лицу 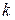 , и число путей длиной 1, ведущих от лица
, и число путей длиной 1, ведущих от лица 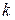 к лицу j:
к лицу j:
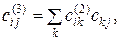 (88)
(88)
или в матричной форме для случаев путей с длиной 3 и 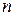 имеем:
имеем:
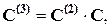 (89)
(89)
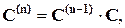 (90)
(90)
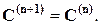 (91)
(91)
Равенство (91) означает, что процесс общения завершается, когда увеличение длины путей не увеличивает количества путей. Если 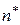 – наименьшее целое число, для которого справедливо (91), то ненулевое значение
– наименьшее целое число, для которого справедливо (91), то ненулевое значение 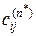 указывает на наличие между субъектами «
указывает на наличие между субъектами « 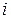 » и «
» и « 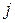 » как минимум одного пути длиной не более
» как минимум одного пути длиной не более 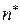 . Равенство
. Равенство 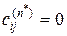 означает, что от субъекта «
означает, что от субъекта « 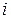 » до субъекта «
» до субъекта « 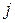 » нет ни одного пути.
» нет ни одного пути.
Выбор типа представления можно отнести к эвристическим способам решения задач. Хорошее представление дает хороший метод решения задач.
ТИПЫ ПРЕДСТАВЛЕНИЙ
На практике довольно широкое распространение получили перечисляющие методы. Перечисляющее представление характеризуетсярассматриваемым множеством U решений задачи и каким-то правилом для их оценки. Независимо от того, U конечно, или бесконечно (но счетное), его элементы в некотором порядке можно порождать, проверять и выбирать правильное решение. При формальном описании перечисления функция 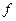 выбирает какое-то одно решение S Î S для любого множества
выбирает какое-то одно решение S Î S для любого множества
S Ê U, а перечисляющий алгоритм выглядит следующим образом.
(1) Положить 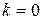 и начать с некоторого множества пробных решений
и начать с некоторого множества пробных решений 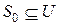 .
.
(2) Если 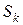 содержит требуемое решение, то работа алгоритма оканчивается. В противном случае перейти к следующему шагу (3).
содержит требуемое решение, то работа алгоритма оканчивается. В противном случае перейти к следующему шагу (3).
(3) Построить 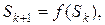 увеличить
увеличить 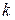 на единицу и перейти к (2).
на единицу и перейти к (2).
Поскольку при реализации перечисляющего метода на каждом шаге выбирается множество Sk+1, зависящее лишь от множества Sk, следующий шаг является функцией рассматриваемого шага и не зависит от его сравнения с ответом. Если характеристики ответа сохраняются одними и теми же, то подразумеваемое сравнение элементов множества Sk с требуемым целевым состоянием можно предусмотреть в самом определении перечисляющей функции f. В машинном доказательстве теорем этот метод оказался действительно полезным.
Решение задач в пространстве состоянийпредполагает существование счетного множества 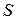 состояний и множества
состояний и множества 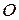 операторов,
операторов,
которые характеризуют связь между различными состояниями. Задача решена, когда найдена такая последовательность операторов
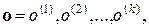 (92)
(92)
что
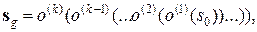 (93)
(93)
где s0 – некоторое состояние из множества начальных состояний, а
sg – из множества целевых состояний. Пусть S будет множеством узлов некоторого графа, у которого узлы i и j соединены дугами тогда и только тогда, когда во множестве O имеется оператор o, отображающий si в sj. Путь от одного состояния к другому эквивалентен соответствующей последовательности операторов.Представлениеввиде графарешения задач приводит к естественному обобщению анализа, при котором учитывается стоимость ck применения оператора ok, что соответствует пометке стоимости каждой дуги графа. При этом во многих случаях каждый последующий поисковый шаг можно выбирать как функцию сравнения целевого и текущего состояний.
Процедура переписывания цепочек похожа на представление, использующее пространство состояний. Здесь возможные «состояния мира», включая начальные и целевые, рассматриваются как правильно построенные выражения некоторого языка. На каждом шаге выбора соответствующего оператора (продукции) структура правильно построенного текущего выражения сравнивается со структурой желаемого. Можно утверждать, что все программные системы решения задач являются системами переписывания цепочек, поскольку содержимое машинной памяти можно выразить в виде цепочки, а любое изменение содержимого памяти есть не что иное, как вывод из нее другой цепочки.
Сведение задачи к подзадачам.В этом методе определяется совокупность подзадач, объединение раздельных решений которых позволяет решить исходную задачу. Этот процесс можно применять рекурсивно для порождения из подзадач других, более тривиальных «задач», решения которых известны, а их объединенное использование приводит к решению более сложной задачи.
Для иллюстрации метода рассмотрим задачу «Ханойская башня». Даны три стержня и три различных диска. Сначала все диски находятся на левом стержне, требуется переместить их все на правый стержень, сохраняя относительное расположение по вертикали (рис. 24). При этом большой диск никогда не должен находиться над меньшим диском. Задача разбивается на две подзадачи. В первой подзадаче учитывается необходимость размещения диска «с» в самом низу стержня 3, для чего диски «а» и «b» в связке перемещаются со стержня 1 на стержень 2, а диск «с» перемещается со стержня 1 на стержень 3.
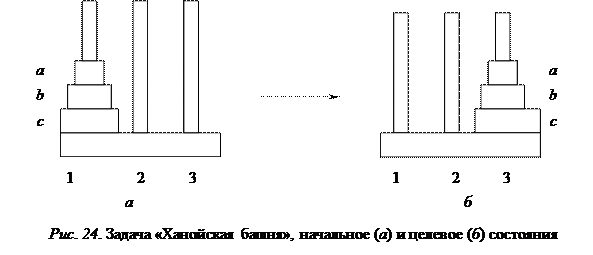
Вторая подзадача решается единственным ходом – перемещением дисков «а» и «b» в связке со стержня 2 на стержень 3. Рассмотренные подзадачи называются «И подзадачами», так как для решения основной задачи они должны быть решены все. Часто возникают случаи «ИЛИ подзадач», т. е. таких задач, что если решается одна из них, то решена и основная.
Дата добавления: 2016-01-20; просмотров: 974;
