ПОИСК ПО КРИТЕРИЮ СТОИМОСТИ
ПОИСК В ШИРИНУ
При этой стратегии в дереве поиска вначале развертывается корневой узел, затем – все его преемники, после этого развертываются преемники этих преемников и т. д. Первоначально развертываются все узлы на данной конкретной глубине, затем происходит развертывание узлов на следующем уровне. Предусматривается, что поверхностные узлы развертываются раньше, чем более глубокие. На рис. 30 показан ход поиска в простом бинарном дереве.
Поиск в ширину является полным, если самый поверхностный целевой узел находится на конечной глубине d и коэффициент ветвления b является конечным. При этих условиях целевой узел обнаруживается после развертывания всех поверхностных (относительно целевого) узлов,
т. е. всегда развертывается самый поверхностный неразвернутый узел. Оптимальность процедуры поиска в ширину может обеспечиваться, когда стоимость пути является неубывающей функцией глубины узла.
Для выявления условий, при которых стратегия поиска в ширину не является оптимальной, определим необходимое время и объем памяти для выполнения поиска. Если в гипотетическом пространстве состояний каждое состояние имеет b преемников, корень дерева поиска вырабатывает b узлов на первом уровне, каждый из которых – еще b узлов. Количество узлов на втором уровне развертывания составляет b2, на третьем уровне – b3 узлов и т. д. Если решение находится на глубине d, необходимо развернуть все узлы, кроме последнего, поскольку сам целевой узел не развертывается, что приводит к выработке bd+1 – b узлов на уровне d + 1. Таким образом, общее количество выработанных узлов равно:
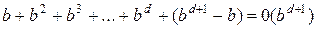 . (95)
. (95)
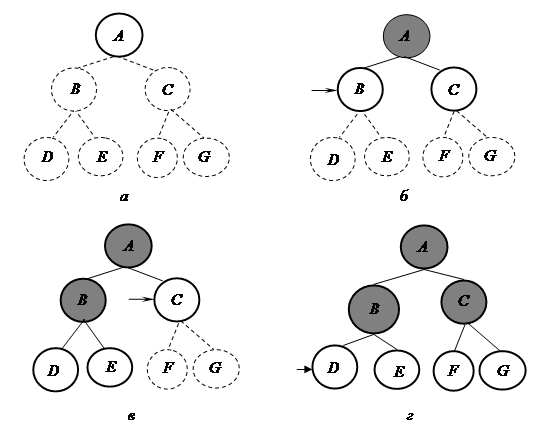
Рис. 30. Поиск в ширину в простом бинарном дереве
(узел, подлежащий развертыванию в следующую
очередь, обозначается маркером)
Поскольку каждый выработанный узел относится к периферии, либо является предком периферийного узла, его необходимо хранить в памяти. Соответственно пространственная сложность становится эквивалентной временной. В табл. 13 приведены требования ко времени и к объему памяти при поиске в ширину при условии, что коэффициент ветвления b = 10, а глубина d решения принимает различные значения от 2 до 10. Данные этой таблицы составлены в предположении, что в секунду формируется
10 000 узлов, а для каждого узла требуется 100 байтов памяти.
Приведенные в табл. 13 данные позволяют сделать вывод о том, что при использовании стратегии поиска в ширину наиболее сложными
могут являться как проблема обеспечения потребности в памяти, так и временной фактор. Например, при ожидании решения важной задачи с глубиной 8 затраты времени, равные 31 часу, не кажутся значительными, но лишь немногие компьютеры имеют терабайт оперативной памяти. В свою очередь, с помощью неинформационных методов сложно или практически невозможно решать задачи поиска с экспоненциальной сложностью.
Таблица 13
Оценки потребности во времени и объеме памяти для
стратегии поиска в ширину при скорости развертывания
10 000 узлов/с и коэффициенте ветвления b = 10
| Глубина | Количество узлов | Время | Память |
| 1 100 | 0,11 с | 1 Мб | |
| 111 100 | 11 с | 106 Мб | |
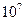
| 19 мин. | 10 Гб | |
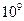
| 31 ч | 1 Тб | |

| 129 сут. | 101 Тб |
ПОИСК ПО КРИТЕРИЮ СТОИМОСТИ
Алгоритм поиск по критерию стоимости является оптимальным не только при одинаковой, но и при любой функции определения стоимости этапа. Вместо развертывания самого поверхностного узла, характерного для собственно поиска в ширину, поиск по критерию стоимости обеспечивает развертывание узла n с наименьшей стоимостью пути, стоимость учитывается не количеством этапов в пути, а их суммарной стоимостью. При условии, что стоимости всех этапов равны, такой поиск полностью идентичен поиску в ширину.
Поскольку в поиске по критерию стоимости учитывается не количество этапов в пути, а только их суммарная стоимость, процедура этого поиска может войти в бесконечный цикл, если в ней может быть развернут узел, имеющий действие с нулевой стоимостью, которое снова указывает на то же состояние. Полноту и оптимальность поиска можно гарантировать при условии, что стоимость каждого этапа больше или равна некоторой небольшой положительной константе 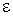 , а алгоритмом поиска реализуется развертывание узлов в порядке возрастания стоимости пути. Выбранный для развертывания первый целевой узел представляет собой оптимальное решение.
, а алгоритмом поиска реализуется развертывание узлов в порядке возрастания стоимости пути. Выбранный для развертывания первый целевой узел представляет собой оптимальное решение.
Если С* – стоимость оптимального решения, а e – минимальная стоимость каждого действия, то пространственно-временную сложность можно оценить величиной 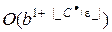 , которая может превосходить значение bd. Последнее имеет место тогда, когда процедура
, которая может превосходить значение bd. Последнее имеет место тогда, когда процедура
поиска по критерию стоимости начинается с анализа коротких путей сложных деревьев, а затем исследуются более длинные пути, соответствующие, возможно, более полезным этапам. Если стоимости всех этапов равны, то 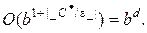
Дата добавления: 2016-01-20; просмотров: 2215;
