Основные теоретические сведения. 2.1.1 Дифференциальное уравнение конвективного теплообмена

2.1.1 Дифференциальное уравнение конвективного теплообмена. Критерии подобия

Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос тепла осуществляется одновременно конвекцией и теплопроводностью. Конвективный теплообмен между потоком жидкости или газа и поверхностью твердого тела называется конвективной теплоотдачей или теплоотдачей.

При практических расчетах теплоотдачи используется закон Ньютона-Рихмана:

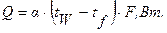
Здесь Q– тепловой поток от стенки к жидкости, Вт; F – поверхность теплообмена, м²; a – коэффициент теплоотдачи, Вт/м²×град; t_W – температура стенки, град; t_f – температура жидкости, град.

Различают вынужденную и естественную конвенцию. В первом случае жидкость или газ движутся за счет внешних для данного процесса сил (насос, ветер и т.д.), во втором случае – за счет разности плотностей нагретых и холодных частиц жидкости.

На процесс конвективного теплообмена существенно влияет характер движения жидкости. Из гидродинамики известно, что имеются два основных режима течения: ламинарный и турбулентный. При ламинарном режиме частицы жидкости движутся, не перемешиваясь; при турбулентном – движутся неупорядоченно, хаотически; направление и величина скорости отдельных частиц непрерывно меняются.

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. В настоящее время точные решения уравнений имеются только для отдельных частных случаев. Поэтому большое значение приобретает экспериментальный путь исследования.

Теоретической базой экспериментальных исследований является теория подобия. С помощью теории подобия размерные физические величины объединяются в безразмерные комплексы, причем так, что число комплексов меньше числа величин, составляющих эти комплексы. Полученные безразмерные комплексы рассматриваются как новые переменные. Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому.

Пусть поверхность твердого тела омывается несжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны соответственно t₀и w₀. Размеры тела ℓ₀ и другие параметры заданы. Температура поверхности тела равна t_W. Примем, что t_W> t₀, а также, что физические параметры тела постоянны. Теплота трения не учитывается. Рассматриваемый процесс является стационарным.

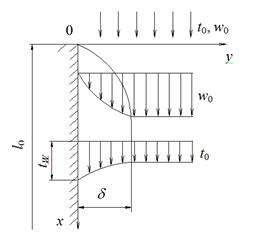
Рисунок 2.1

Расположим оси координат так, как показано на рисунке 2.1. Ось z направлена перпендикулярно плоскости чертежа.

При принятых условиях конвективный теплообмен описывается системой дифференциальных уравнений:

уравнение теплоотдачи:

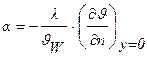, (2.2)

где J = t - t₀, t – температура жидкости; J_W = t_W - t₀; n – нормаль к поверхности;

уравнение энергии:

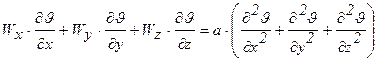(2.3),

где 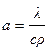- коэффициент температуропроводности жидкости,

r, с – соответственно, плотность и удельная теплоемкость жидкости;

уравнения движения:

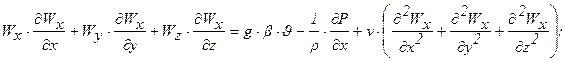(2.4а)

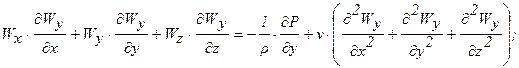(2.4б)

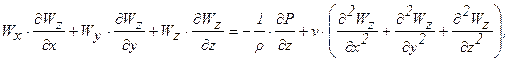(2.4в)

где Р – давление жидкости,

n - коэффициент кинематической вязкости жидкости;

уравнение неразрывности:

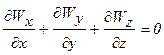. (2.5)

Граничные условия:

1. Вдали от тела (х<0):

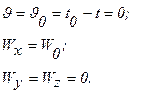(2.6)

2. На поверхности тела (у=0; 0£х£ℓ₀):

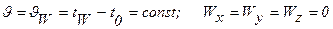. (2.7)

В уравнениях и условиях однозначности различают три вида величин:

независимые переменные – координаты x, y, z;

зависимые переменные – a, J, W_x, W_y, W_z и P; они однозначно определяются значениями независимых переменных, если заданы величины, входящие в условия однозначности;

постоянные величины – W₀, t₀, ℓ₀, J_c, n, a, l, b, r и др., они задаются условиями однозначности и для определенной задачи являются постоянными величинами, не зависящими от других переменных; от задачи к задаче они могут меняться.

Таким образом, искомые зависимые переменные a, J, W_x, W_y, W_z и P зависят от большого числа величин: они являются функциями переменных и постоянных величин, входящих в условия однозначности.

Величины, содержащиеся в уравнениях и условиях однозначности, можно сгруппировать в безразмерные комплексы. Число безразмерных комплексов будет меньше числа размерных величин. Для приведения уравнений и условий однозначности к безразмерному виду выбирают масштабы приведения. В качестве масштабов удобно принять постоянные величины, входящие в условия однозначности.