Примеры решения задач по теплопроводности.
Задача 1. Определить количество теплоты, которое передается в течение 1 часа через стенки картера авиадвигателя, если толщина стенок d = 5,5 мм, площадь поверхности стенок F = 0,6 м2, температура на внутренней поверхности картера tW1= 75°С, на наружной tW2= 68°С, а средний коэффициент теплопроводности стенок
l= 175 Вт/м×град.
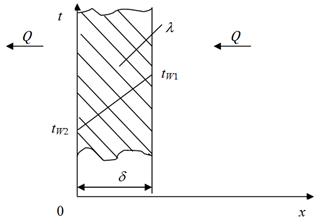
Рисунок 1.6
Решение : Количество теплоты, передаваемое через стенки картера в течение 1 часа, будет равно:
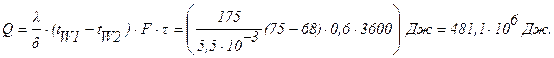
Задача 2. Вычислить плотность теплового потока через плоскую однородную стенку(l - коэффициент теплопроводности), толщина которой значительно меньше ширины и высоты, если стенка выполнена:
а) из стали (l= 40 Вт/м×град);
б) из бетона (l= 1,1 Вт/м×град);
в) из кирпича (l= 0,11 Вт/м×град).
Во всех трех случаях толщина стенки d =50 мм. Температуры на поверхностях стенки поддерживаются постоянными и равными tW1=100°С и tW2=90°С.
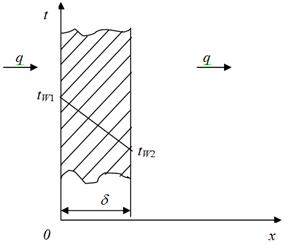
Рисунок 1.7
Решение: Плотность теплового потока q определяется выражением (1.6):
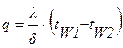 .
.
Откуда:
для стенки из стали  ;
;
для стенки из бетона  ;
;
для стенки из кирпича 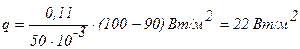 .
.
Задача 3. Определить толщину тепловой изоляции d, выполненной из:
1) альфоля;
2) шлаковой ваты.
Удельные потери теплоты через изоляционный слой q =523 Вт/м2, температуры его поверхности tW1=700°C и tW2=40°C. Коэффициент теплопроводности альфоля l= 0,0302+0,000085×t и коэффициент теплопроводности шлаковой ваты
l= 0,058+0,000145×t. Здесь t – средняя температура изоляции в °C.
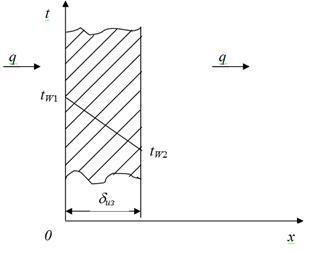
Рисунок 1.8
Решение: В случае линейной зависимости коэффициента теплопроводности от температуры плотность теплового потока определяется по формуле для постоянного коэффициента теплопроводности, взятого при средней температуре стенки /20, задача 1-6/, т.е.:

Определяем lср альфоля:

Определяем толщину альфолиевой изоляции:

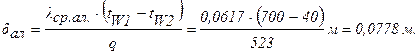
Определяем lср шлаковой ваты:
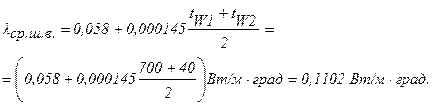
Толщина тепловой изоляции из шлаковой ваты:
 .
.
Задача 4. Плоская стенка (коэффициент теплопроводности l = 11,6 Вт/м×град, толщина d = 0,005 м) омывается с одной стороны горячими газами с температурой
tf1 = 2000°С, а с другой стороны охлаждается водой с tf2 = 27°С. Коэффициенты теплоотдачи от газа к стенке a1 = 467 Вт/м2×град, от стенки к воде
a2 = 3500 Вт/м2×град. Определить удельный тепловой поток и температуры стенки tW1, tW2.

Рисунок 1.9
Решение : Удельный тепловой поток через стенку равен (формула 1.12):
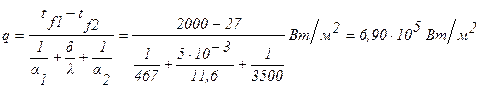 .
.
Температуры стенок определяются (формулы 1.10, 1.11):
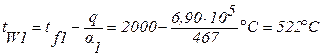 ;
;
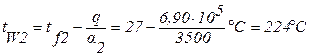 .
.
Задача 5. Определить удельный тепловой поток с учетом и без учета теплового сопротивления контакта через многослойную плоскую стенку, состоящую из слоя окиси циркония толщиной d1 = 0,2 мм, слоя стали толщиной d2 = 6 мм, слоя алюминия толщиной d3=10мм, если температуры на внешних поверхностях стенки поддерживаются постоянными и равными tW1 = 1200°С и tW4 = 400°С; коэффициент теплопроводности окиси циркония l1 = 1,15 Вт/м×град, стали l2 = 34,9 Вт/м×град и алюминия l3 = 422 Вт/м×град. Термическое сопротивление контакта между слоями окиси циркония и стали Rк1 = 0,258×10-3 м2град/Вт, а между слоями стали и алюминия Rк2 = 0,266×10-3 м2град/Вт. Определить температуры на контактирующих поверхностях каждого слоя.
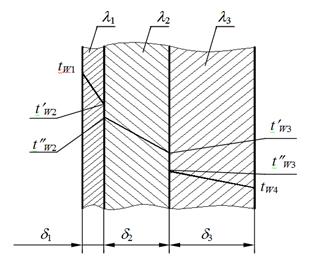
Рисунок 1.10
Решение: Для трехслойной стенки при стационарной теплопроводности с учетом теплового сопротивления контакта удельный тепловой поток определяется выражением (формула 1.9 для n-слойной стенки):

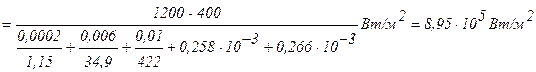 .
.
Для трехслойной стенки без учета теплового сопротивления удельный тепловой поток определяется формулой (1.7), т.е.:
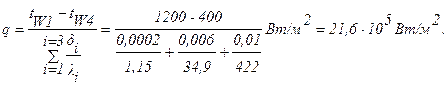
Температуры на контактирующих поверхностях будут равны:


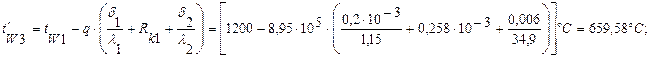

Задача 6. Змеевики пароперегревателя выполнены из труб жаропрочной стали диаметром d1/d2=32/42 мм с коэффициентом теплопроводности l=14 Вт/м×град. Температура внешней поверхности трубы tW2=580°С, внутренней – tW1=450°С. Вычислить удельный тепловой поток через стенку на единицу длины трубы.
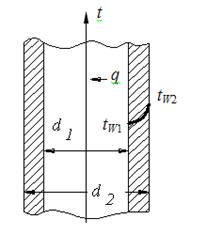
Рисунок 1.11
Решение: Поток тепла, проходящий через единицу трубы, представляющей собой цилиндрическую стенку, равен (формула 1.18):

Задача 7. Паропровод диаметром 150/160 мм покрыт слоем тепловой изоляции толщиной dиз=100мм. Коэффициенты теплопроводности стенок трубы
l1=50 Вт/м×град и изоляции l2=0,08 Вт/м×град. Температура на внутренней поверхности паропровода tW1=400°С и на наружной поверхности изоляции tW3=50°С. Найти тепловые потери с 1 м паропровода и температуру на границе соприкосновения паропровода и изоляции tW2.
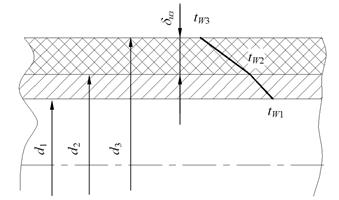
Рисунок 1.12
Решение: Внешний диаметр паропровода равен:
 .
.
Тепловые потери с 1м паропровода будут равны (формула 1.19):
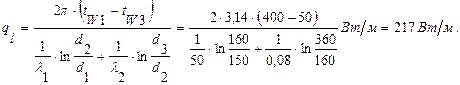
Температура tW2 будет равна (из формулы 1.18):

Задача 8. Определить температуры на поверхности соприкосновения слоев стенки tW2 камеры сгорания жидкостного ракетного двигателя и на внешней поверхности tW3, если диаметр камеры d1=190 мм, толщина защитного покрытия dn=1 мм и его коэффициент теплопроводности ln=1,15 Вт/м×град, а толщина основной стенки
dW=2 мм и ее коэффициент теплопроводности lW=372 Вт/м×град. Удельный тепловой поток q=407500 Вт/м2, температура на поверхности покрытия со стороны камеры tW1=1200°С.
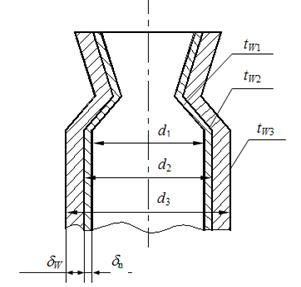
Рисунок 1.13
Решение: Из формул (1.18) и (1.19) будем иметь:
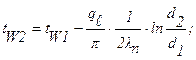
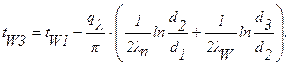
Из условий задачи:
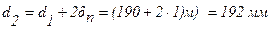 ;
;
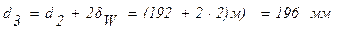 ;
;
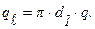
Тогда:
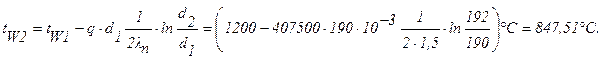
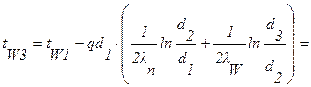
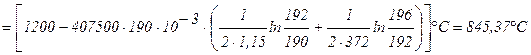 .
.
Задача 9. По неизолированному трубопроводу диаметром 170/185 мм, проложенному на открытом воздухе, протекает вода со средней температурой tf1= 95°С, температура окружающего воздуха tf2= -18°С. Определить потерю теплоты с 1м длины трубопровода и температуры на внутренней и внешней поверхностях этого трубопровода, если коэффициент теплопроводности материала трубы
l=58,15 Вт/м×град, коэффициент теплоотдачи от воды к стенке трубы
a1=1395 Вт/м×град и от трубы к окружающему воздуху
a2= 13,95 Вт/м×град.
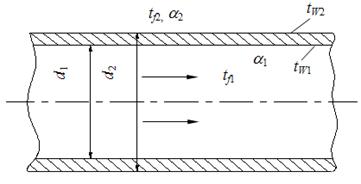
Рисунок 1.14
Решение: Потеря тепла с 1м длины трубопровода будет равна (формула 1.21):

Температуры на внутренней и внешней поверхностях практически равны (формулы для определения температур аналогичны выражениям (1.10), (1.11) для плоской стенки):
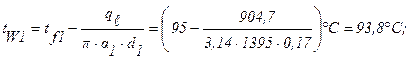

Задача 10. Определить тепловые потери на 1м длины трубопровода, а также температуры на внутренней и внешней поверхностях при условии, что трубопровод, рассматриваемый в задаче 1.9, покрыт слоем изоляции толщиной d =70 мм с коэффициентом теплопроводности lиз= 0,116 Вт/м×град, а коэффициент теплоотдачи поверхности изоляции к окружающей среде a2=9,3 Вт/м2×град. Остальные условия те же, что и в задаче 1.9.

Рисунок 1.15
Решение: В соответствии с условиями задачи
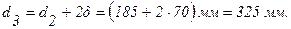
Тепловые потери на 1 м длины трубопровода можно определить по формуле (1.22):
lиз=l2;

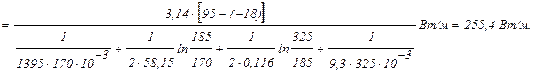
Температуры на поверхностях трубопровода будут равны:


Задача 11. Шаровой реактор, внутренний диаметр которого d1 = 1м, имеет общую толщину стенки и слоя изоляции d = 65мм с эквивалентным коэффициентом теплопроводности lэкв = 1,047 Вт/м×град. Определить удельную тепловую нагрузку внутренней и наружной поверхностей стенки реактора, если температура внутренней поверхности стенки tW1 = 160°С, а внешней tW2= 60°С.
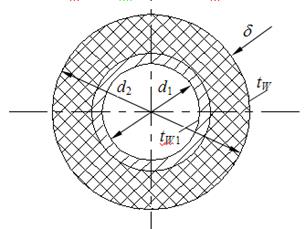
Рисунок 1.16
Решение: Из условий задачи: d2= d1 +2d =(1000+2×65) мм=1130 мм.
Общее количество теплоты, выделяемое реактором (формула 2.63 /14/):

Удельная тепловая нагрузка на внутренней и наружной поверхностях:

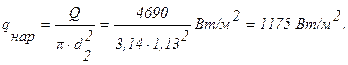
Задача 12. Электронагреватель выполнен из нихромовой проволоки диаметром d = 2 мм, длиной l = 10 м. Он обдувается холодным воздухом с температурой t = 20°С. Вычислить тепловой поток с 1 м нагревателя, а также температуры на поверхности и на оси проволоки, если сила тока I, проходящего через нагреватель, составляет 25А. Удельное электрическое сопротивление нихрома r =1,1 Ом×мм2/м, коэффициент теплопроводности нихрома l =17,5 Вт/м2×град и коэффициент теплоотдачи от поверхности нагревателя к воздуху a=46,5Вт/м2×град.
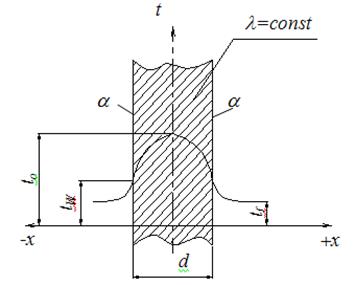
Рисунок 1.17
Решение: Электрическое сопротивление нагревателя:
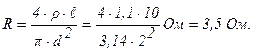
Мощность нагревателя:
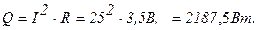
Тепловой поток, выделяемый нагревателем на длине 1 м:

Температура поверхности проволоки будет равна:

Температура на оси проволоки нагревателя равна
(из формулы 2-147 /14/):
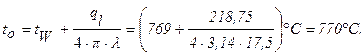
Задача 13. Трубка из нержавеющей стали с внутренним диаметром d1= 7,6 мм и наружным диаметром d2= 8 мм включена в электрическую цепь. Все тепло отводится через внутреннюю поверхность трубки. Вычислить объемную производительность источников тепла и перепад температур в стенке трубки, если по трубке пропускается ток силой I=250 А. Удельное электрическое сопротивление и коэффициент теплопроводности стали соответственно равны r=0,85 Ом×мм2/м, l =18,6 Вт/м×град.
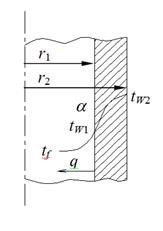
Рисунок 1.18
Решение: Электрическое сопротивление на единицу длины трубки:

Здесь r1, r2 – внутренний и внешний радиусы трубки (r1 =7,6 мм, r2=4 мм).
Тепловой поток на единицу длины:
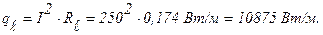
Объемная производительность внутренних источников тепла:
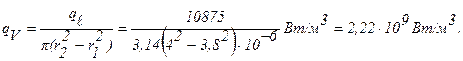
Перепад температур в стенке трубы (формула 1.35):

Задача 14. Через трубку из нихромовой стали диаметром 14/14,6 мм пропускается ток силой I=300А. Определить объемную теплопроизводительность источников теплоты и перепад температуры в стенке трубки в предположении, что теплота отводится:
а) только через внутреннюю поверхность трубки;
б) только через наружную поверхность трубки.
Электрическое сопротивление материала трубки r =1,17 Ом×мм2/м и коэффициент теплопроводности l = 7,2 Вт/м×град.
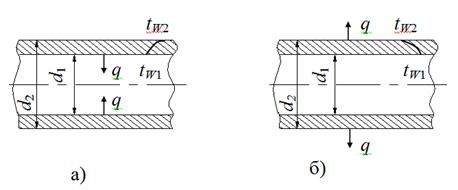
Рисунок 1.19
Решение: Электрическое сопротивление на единицу длины трубки:
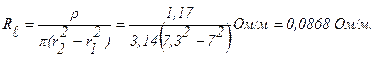
Здесь r1=7 мм и r2=7,3 мм – внутренний и внешний радиусы трубки.
Тепловой поток на единицу длины:
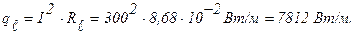
Объемная производительность внутренних источников тепла:
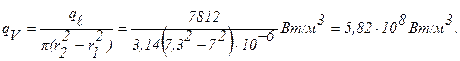
а) Перепад температур в стенке трубки при отводе теплоты через внутреннюю поверхность трубки (формула 1.35):
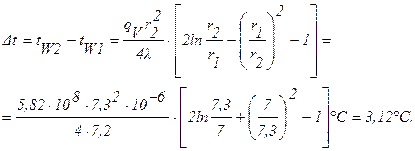
б) Перепад температур в стенке трубки при отводе теплоты через наружную поверхность трубки (формула 1.32¢):

Задача 15. Вычислить максимальное значение температуры тепловыделяющего элемента (ТВЭЛ) ядерного реактора, имеющего форму неограниченной плоской пластины. Производительность равномерно распределенных по объему пластины внутренних источников тепла qV =90 МВт/м3,температуры поверхности пластины равны tW1 =1500°С и tW2 =2000°С, толщина пластины d =20 мм. Коэффициент теплопроводности материала пластины l = 17 Вт/м×град. Также определить закон изменения температуры внутри пластины и расстояние х0 от поверхности пластины с температурой tW1 до сечения, в котором t = tmax.

Рисунок 1.20
Решение: Уравнение стационарной теплопроводности для плоской пластины с внутренними источниками тепла:

Граничные условия:
при х = 0 t=tW1;
при х = d t=tW2.
Общее решение уравнения (формула 2-133/14/):

Постоянные интегрирования С1 и С2 будут равны:
С2 = tW1.
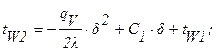
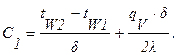
Откуда:
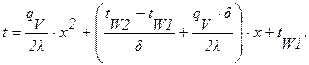
Максимальное значение температуры будет при х=х0.
В точке х=х0 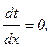 т.е.:
т.е.:
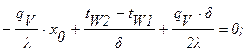
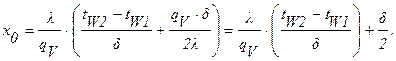
Производим вычисления:

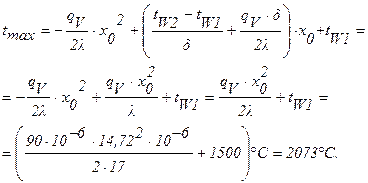
Задача 16. Рассчитать распределение температуры в поперечном сечении тепловыделяющего элемента (ТВЭЛ), имеющего форму длинного полого цилиндра с внутренним диаметром d1=16 мм и наружным d2=26 мм, выполненного из урана. Коэффициент теплопроводности урана lу= 31 Вт/м×град. Обе поверхности ТВЭЛа покрыты плотно прилегающими оболочками из нержавеющей стали толщиной
d =0,5 мм. Коэффициент теплопроводности нержавеющей стали lст=21 Вт/м×град. Объемная плотность тепловыделения в уране принята равномерной по сечению и равной qV=5×107 Вт/м3. ТВЭЛ охлаждается газообразной двуокисью углерода СО2, движущейся по внутреннему каналу с внешней стороны ТВЭЛа. Среднемассовая температура СО2 во внутреннем канале tf1=200°С, во внешнем канале tf2 =240°С. Коэффициенты теплоотдачи от поверхностей оболочек к газу соответственно равны a1=520 Вт/м2×град и a1=560Вт/м2×град. Определить максимальную температуру ТВЭЛа t0, температуры на поверхностях оболочек tW1 и tW2 и на поверхностях урана t1 и t2.
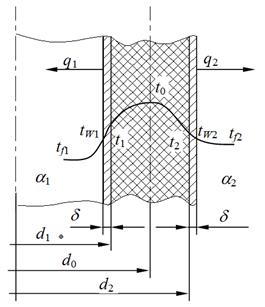
Рисунок 1.21
Решение: Тепло отводится через внутреннюю и наружную поверхности ТВЭЛа. При двусторонней теплоотдаче внутри цилиндрической стенки существует максимум температуры. Изотермическая поверхность, соответствующая максимальной температуре t0, разделяет цилиндрическую стенку на два слоя. Во внутреннем слое тепло q1 передается внутрь трубы, во внешнем слое тепло q2 отводится наружу. Максимальной температуре соответствует диаметр d0 или радиус r0. Максимальные перепады температур во внешнем и внутренних слоях цилиндрической урановой стенки определяются уравнениями (формулы 1.32¢, 1.35):
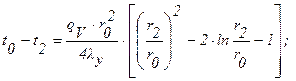
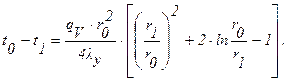
Здесь r1 и r2, соответственно, внутренний и внешний радиусы цилиндрической стенки.
Из совместного решения этих уравнений для r0 получим:
 .
.
Введем в рассмотрение эффективные коэффициенты теплоотдачи от поверхностей ТВЭЛа к охлаждающему газу во внутреннем и внешнем каналах ТВЭЛа aэф1 и aэф2 по выражениям:
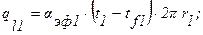

где


Совместное решение этих уравнений относительно r0 приводит к выражению:
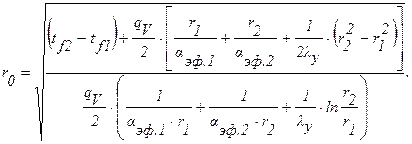
Для цилиндрической стенки тепловые сопротивления теплоотдачи на соответствующих поверхностях, определяемых диаметрами d1, d2, d1-2d, d2+2d, будут соответственно равны:

Тепловые сопротивления внутренней и внешней стенки будут равны соответственно:
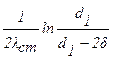 ,
, 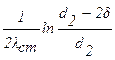 .
.
Из условий теплового баланса будем иметь:

Или:
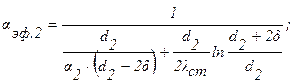

Подставляя численные значения переменных, получим:

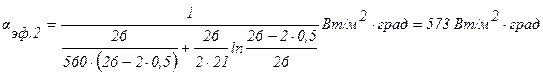
Откуда:
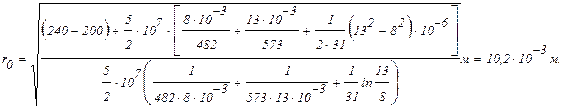
Плотность теплового потока на внутренней поверхности урана равна:
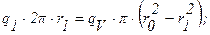
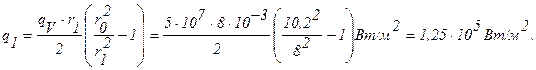
Температура на внутренней поверхности урана:
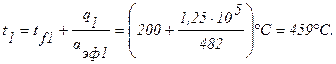
Плотность теплового потока на внутренней поверхности оболочки:

Температура на внутренней поверхности оболочки:
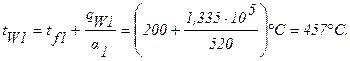
Плотности теплового потока q2 и qW2 и температура t2 и tW2 на внешней поверхности ТВЭЛа определяются аналогично:
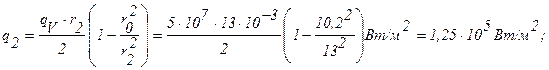
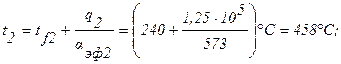
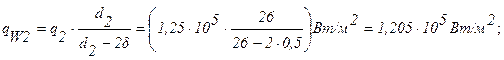
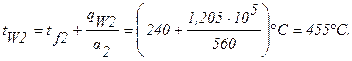
Распределение температуры по сечению ТВЭЛа определяется уравнением (формула 1.34, r2=r0):
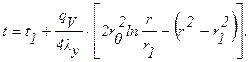
Тогда:
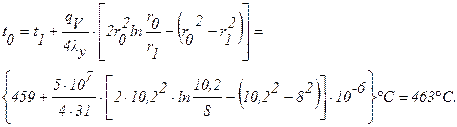
Дата добавления: 2015-12-26; просмотров: 108906;
