Основные теоретические сведения

1.1.1 Дифференциальное уравнение теплопроводности

Аналитическая теория теплопроводности игнорирует молекулярное строение вещества и рассматривает вещество как сплошную среду (континуум). В жидкостях и газах чистая теплопроводность может быть реализована при выполнении условий, исключающих перенос тепла конвекцией.

Исследование теплопроводности сводится к изучению пространственно-временного изменения температуры тела, т.е. к нахождению уравнения температурного поля:

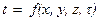. (1.1)

Различают стационарные и нестационарные температурные поля. Выражение (1.1) отвечает неустановившемуся режиму теплопроводности и носит название уравнения нестационарного температурного поля.

Дифференциальное уравнение нестационарной теплопроводности записывается в виде:

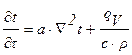, (1.2)

где 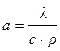– коэффициент температуропроводности вещества, м²/с;

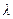– коэффициент теплопроводности вещества, Вт/м×град;

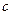– удельная теплоемкость вещества, Дж/кг×град;

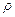– плотность вещества, м³/кг;

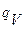– удельная объемная производительность внутренних источников тепла, Вт/м³;

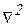– оператор Лапласа.

В декартовой системе координат: .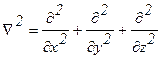

Частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности, или краевыми условиями.

Условия однозначности включают в себя:

а) геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;

б) физические условия, характеризующие физические свойства среды и тела;

в) временные и начальные условия, характеризующие распределение температур в изучаемом теле в начальный момент времени;

г) граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.

Граничные условия могут быть заданы следующими способами:

а) граничные условия первого рода – задание на поверхности тела температуры для каждого момента времени;

б) граничные условия второго рода – задание величины теплового потока для каждой точки поверхности тела и любого момента времени;

в) граничные условия третьего рода – задание температуры окружающей среды и закона теплообмена между поверхностью тела и окружающей средой;

г) граничные условия четвертого рода – условия теплообмена системы тел или тела с окружающей средой по закону теплопроводности. Предполагается, что между телами осуществляется идеальный контакт (температуры соприкасающихся поверхностей одинаковы).

При стационарном тепловом режиме температура тела остается постоянной во времени. Дифференциальное уравнение теплопроводности будет иметь вид:

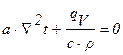, (1.3)

или

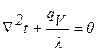. (1.3¢)

Если внутренние источники тепла отсутствуют ( 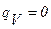), то уравнение (1.3¢) упростится и примет вид:

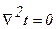, (1.4)

или в декартовой системе координат:

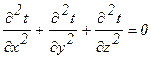. (1.5)

1.1.2 Передача тепла через плоскую стенку ( )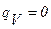

Рассмотрим однородную и изотропную стенку толщиной d с постоянным коэффициентом теплопроводности l (рисунок 1.1):

1.1.2.1 Граничные условия первого рода

На наружных поверхностях стенки температуры поддерживаются постоянными и равными:

при х = 0 t = t_W1;

при х = d t = t_W2.

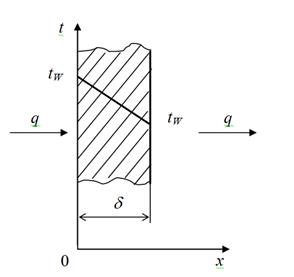
Рисунок 1.1 - Однородная плоская стенка

Удельный тепловой поток, или плотность теплового потока, т.е. количество тепла, проходящего через единицу поверхности стенки в единицу времени, будет равно:

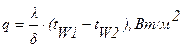. (1.6)

Для многослойной плоской стенки, состоящей из п однородных слоев, принимая во внимание, что контакт между слоями совершенный и температура на соприкасающихся поверхностях двух слоев одинакова, удельный тепловой поток будет равен:

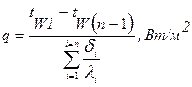. (1.7)

где i – номер слоя.

Удельный тепловой поток через поверхность контакта можно выразить формулой:

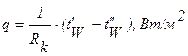, (1.8)

где R_k – термическое сопротивление контакта;

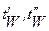- температуры контактирующих поверхностей.

Удельный тепловой поток через отдельные слои и поверхности контактов равен:

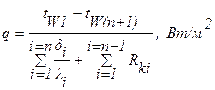. (1.9)

1.1.2.2 Граничные условия третьего рода (теплопередача)

Передача тепла от одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде.

Рисунок 1.2 – Теплопередача через однородную плоскую стенку

Пусть плоская однородная стенка имеет толщину d (рисунок 1.2). Заданы коэффициент теплопроводности стенки l, температуры окружающей среды t_f1, t_f2, а также коэффициенты теплоотдачи a₁, a₂; будем считать, что величины a₁, a₂, t_f1, t_f2постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменения температур жидкостей и стенки только в направлении, перпендикулярном плоскости стенки.

Коэффициенты теплоотдачи определяют интенсивность теплоотдачи от горячей жидкости к стенке и от второй поверхности стенки к холодной жидкости в соответствии с выражениями:

q=a₁×(t_f1-t_W1); (1.10)

q=a₂×(t_f2-t_W2). (1.11)

Удельный тепловой поток q от одной жидкости к другой через разделяющую их стенку будет равен:

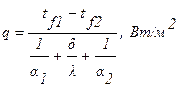. (1.12)

Обозначим:

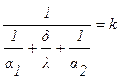. (1.13)

Тогда:

. (1.14)

Величина k называется коэффициентом теплопередачи и имеет ту же размерность, что иa₁, a₂, т.е. Вт/м²×град.

Удельный тепловой поток через многослойную стенку, состоящую из n слоев, будет равен:

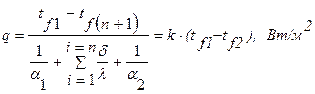. (1.15)

С учетом термических сопротивлений между отдельными слоями удельный тепловой поток многослойной стенки будет равен:

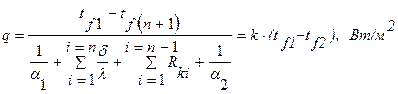, (1.16)

где R_ki – термическое сопротивление i-слоя;

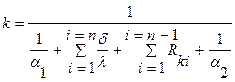. (1.17)

1.1.3 Передача тепла через цилиндрическую стенку (q_V=0)

а) б)

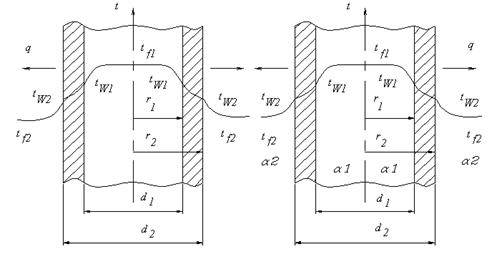
Рисунок 1.3 – Теплопроводность цилиндрической стенки при граничных
условиях первого (а) и второго (б) рода

Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d₁=2r₁ и наружным диаметром d₂=2r₂ при граничных условиях первого рода. Расчетная формула для определения удельного теплового потока q_ℓ, проходящего через единицу длины трубы записывается в виде:

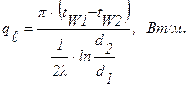(1.18)

Для многослойной цилиндрической стенки, состоящей из однородных слоев, имеем:

- без учета термических сопротивлений контактов:

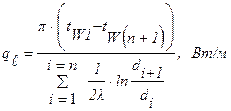. (1.19)

- с учетом термических сопротивлений контактов R_Ki:

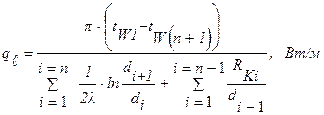. (1.20)

При граничных условиях третьего рода линейные плотности теплового потока будут равны

- для однородной однослойной стенки

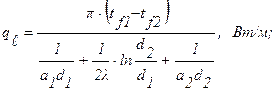(1.21)

- для многослойной стенки без учета термических сопротивлений контактов:

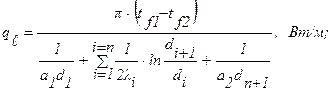(1.22)

- для многослойной стенки с учетом термических сопротивлений контактов R_Ki:

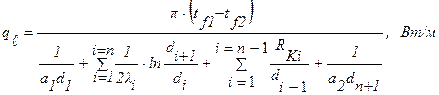. (1.23)

1.1.4 Теплопроводность при наличии внутренних источников тепла

1.1.4.1 Теплопроводность однородной пластины

Рассмотрим длинную пластину, толщина которой 2d - величина малая по сравнению с двумя другими размерами.

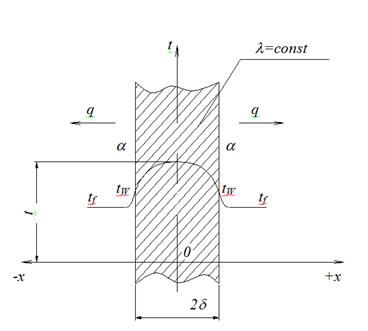
Рисунок 1.4 - Теплопроводность плоской пластины при наличии внутреннего источника тепла

Источники тепла равномерно распределены по всему объему пластины. Плотность объемного тепловыделения q_V= const. Заданы коэффициент теплоотдачи a и температура жидкости вдали от пластины t_f, причем a=const и t_f =const. При указанных условиях температура пластины будет изменяться только вдоль оси х.

Дифференциальное уравнение (1.3¢) принимает вид:

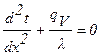. (1.24)

Граничные условия:

при х = 0 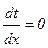(1.25)

при х =±d 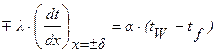. (1.26)

Тогда для распределения температуры по толщине пластины будем иметь:

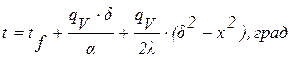, (1.27)

Тепловой поток с единицы поверхности пластины при х=d будет равен:

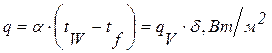. (1.28)

1.1.4.2 Теплопроводность цилиндрической стенки

Рассмотрим бесконечно длинную цилиндрическую стенку (трубу) с внутренним радиусом r₁, наружным r₂ и постоянным коэффициентом теплопроводности l (рисунок 1.5). Внутри этой стенки равномерно распределены источники тепла производительностью q_V. Коэффициенты теплоотдачи a₁ и a₂.

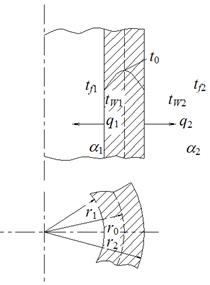
Рисунок 1.5 - Отвод теплоты внутренних источников через поверхности цилиндрической стенки (теплота отводится через обе поверхности)

В такой стенке температура будет изменяться только в направлении радиуса, и процесс теплопроводности будет описываться уравнением:

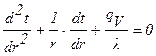. (1.29)

Интеграл этого уравнения:

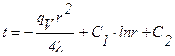. (1.30)

Постоянные интегрирования С₁, С₂ определяются из граничных условий.

Рассмотрим случаи, когда теплоотдающей поверхностью являются только внутренняя или только наружная поверхность, или обе поверхности одновременно.

а) Тепло отводится только через наружную поверхность трубы

При граничных условиях третьего рода на наружной поверхности трубы для распределения температур по толщине трубы будем иметь выражение:

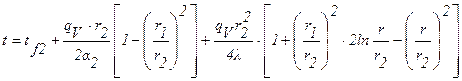(1.31)

При граничных условиях первого рода на наружной поверхности трубы для распределения температур по толщине трубы будем иметь:

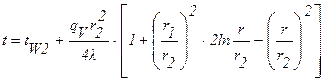. (1.32)

Перепад температур в стенке трубы:

. (1.32¢)

б) Тепло отводится только через внутреннюю поверхность трубы

При граничных условиях третьего рода на внутренней поверхности трубы для распределения температур по толщине трубы имеем выражение:

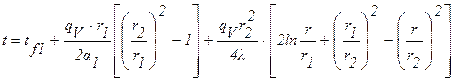. (1.33)

При граничных условиях первого рода на внутренней поверхности трубы для распределения температур по толщине трубы имеем выражение:

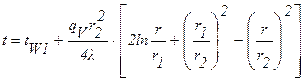. (1.34)

Перепад температур в стенке трубы:

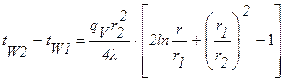. (1.35)

в) Тепло отводится через внутреннюю и наружную поверхности

Для решения этой задачи используются соотношения (1.31) - (1.34).

Необходимо знать радиус r₀ (рисунок 1.5), соответствующий максимальной температуре t₀. Максимальное значение температуры соответствует условию
dt/dr =0и, следовательно, q=0. Тогда при граничных условиях первого рода:

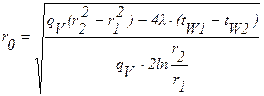. (1.36)

Для нахождения распределения температуры при граничных условиях первого рода во внутреннем слое трубы (r₁ < r < r₀) в уравнение (1.34) подставляются значения текущей координаты r, а для нахождения распределения температуры во внешнем слое в уравнение (1.32) подставляются значения r₀ < r < r₂.