ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

ОБЩИЕ УКАЗАНИЯ О ПОТЕРЯХ НАПОРА.

К потоку могут быть приложены различные внешние силы, имеющие некоторые перемещения: такие силы будут совершать работу и изменять величину механической энергии, несомой жидкостью. Например, поток воды может приводить в действие гидравлическую турбину, причем полная механическая энергия потока за счет работы лопастей турбины будет уменьшаться; стенки металлического напорного трубопровода могут вибрировать, причем эта вибрация будет «поглощать» энергию, несомую жидкостью, и т.п. Мы далее не будем касаться таких случаев. Далее будем иметь в виду потерю механической энергии потоком, находящимся в неподвижном русле, обусловленную работой только сил трения, возникающих в реальной жидкости при ее движении (см. § 4-2; конец п. 1۫ ). Именно эту потерю энергии («потерю напора») мы учитывали выше при рассмотрении уравнения Бернулли. Различают два вида такого рода потерь напора:

1) так называемую потерю напора по длине. Она распределяется по длине потока равномерно (при равномерном движении) или несколько неравномерно (при плавно изменяющемся неравномерном движении). Такую потерю напора, получающуюся на длине l потока, будем обозначать через h_l;

2) так называемые местные потери напора, получающиеся только в отдельных местах потока, где поток претерпевает ту или другую резкую местную деформацию. Каждую отдельную местную потерю напора будем обозначать через h_j.

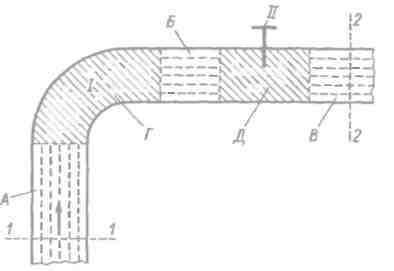
Рис. 4-1. Области, внутри которых напряжения трения τ распределяются: a — равномерно — см. области А, Б, В — здесь получаются “потери напора по длине”; б — неравномерно (беспорядочно) — см. области Г и Д — здесь получаются “местные потери напора”

На рис. 4-1 представлен трубопровод, имеющий особые узлы: поворот I, задвижку II (частично открытую). Помимо потери напора по длине между сечениями 1-1 и 2-2 (на участках А, Б, В), в данном случае будут еще две местные потери напора: на участках Г и Д, где происходит местная деформация потока, причем, как это будет пояснено ниже, в них получается резко изменяющееся неравномерное движение жидкости.

На участке потока, где имеют место «потери по длине», касательные напряжения трения τ распределяются вдоль потока равномерно или примерно равномерно; на участках же потока, где имеют место «местные потери», напряжения τ распределяются резко неравномерно.

Часто длина потока в пределах участков Г и Д (рис. 4-1) является пренебрежимо малой по сравнению с длиной остальной части потока. Поэтому при выполнении практических расчетов обычно считают, что суммарная длина участков, в пределах которых имеются «местные потери напора», равна нулю; «потери же напора по длине» имеют место на длине всего потока. При такой постановке вопроса (которой мы далее и будем придерживаться) любую местную потерю следует относить, выполняя практические расчеты, к соответствующему поперечному сечению потока (а не к участку его некоторой протяженности).

В общем случае для участка трубопровода, заключенного между двумя сечениями (рис. 4-1), пишут:

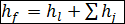(4-1)

где величина h_f может быть названа полной потерей напора для рассматриваемого участка трубы.

Заметим, что в гл. 3 на рис. 3-28, 3-29, 3-30 под величиной h_f следовало бы, собственно, понимать потерю h_l.

В результате работы сил трения, представленных касательными напряжениями τ, механическая энергия, несомая жидкостью, переходит в тепло, причем жидкость нагревается; тепло с течением времени рассеивается.

Можно сказать, что величина потери напора h_f есть мера той механической энергии жидкости, несомой единицей ее веса, которая благодаря работе сил трения, распределенных равномерно по длине потока, а также сосредоточенных в отдельных его узлах («местных сил трения»), переходит в тепло и безвозвратно теряется потоком.

В гидравлике часто пользуются термином «гидравлические сопротивления». Под этим термином следует понимать силы трения, возникающие в реальной жидкости при ее движении. При движении идеальной жидкости силы трения, а следовательно, и касательные напряжения трения равны нулю; поэтому мы можем сказать, что в случае идеальной жидкости силы гидравлического сопротивления отсутствуют.

Чем больше силы трения в реальной жидкости, тем больше, при равных прочих условиях, потери напора h_f. Между силами трения и потерями напора h_f (т. е. работой сил трения) существует, естественно, определенная зависимость. Зная распределение в потоке напряжений τ, а также скоростей и (дающих нам величину перемещений частиц жидкости), мы могли бы подсчитать работу сил трения и тем самым определить потери напора. Однако такая задача является весьма трудной, в частности, в связи с тем, что поле скоростей и нам часто бывает неизвестным. Здесь приходится идти особыми приближенными путями, освещаемыми ниже. При этом, рассматривая вначале простейший случай движения жидкости — установившееся равномерное движение (местные потери отсутствуют) — мы пользуемся особым уравнением, которое дает связь только между силами трения и потерями напора. Это достаточно точное уравнение принято называть основным уравнением установившегося равномерного движения жидкости (см. § 4-2). На основании этого уравнения, а также на основании законов Ньютона о силах внутреннего трения (см. § 4-3), мы далее и устанавливаем необходимую нам зависимость, связывающую потери напора и скорости движения жидкости. Этот вопрос достаточно хорошо решается теоретически для простейших случаев ламинарного движения (см. § 4-4 и 4-5). В случае турбулентного режима приходится прибегать к использованию некоторых экспериментальных коэффициентов, вводимых в теоретический анализ.

Что касается потерь напора при неустановившемся движении (см. гл. 9), а также при установившемся неравномерном движении жидкости, то отыскание зависимости, связывающей потери напора и скорости движения жидкости, является особенно трудной задачей. Поэтому часто потери напора здесь приходится определять, пользуясь формулами, относящимися к установившемуся равномерному движению. При таком условном использовании этих формул в них иногда вводят некоторые коррективы.