Вынужденные колебания без сопротивления. Биения, резонанс.

Предположим, что наряду с восстанавливающей силой на систему действует еще возмущающая сила, являющаяся заданной функцией времени. Рассмотрим сначала наиболее простой случай периодиче­ской возмущающей силы Q(t), изменяющейся по гармоническому закону: Q(t) = Н sin (pt+α), где Н—амплитуда, р — частота, α — начальная фаза возмущающей силы. При наличии возмущающей силы дифференциальное уравнение дви­жения будет иметь вид

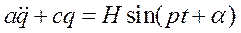
или, если разделить обе части на а,

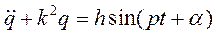(5.14)

где, как и раньше, 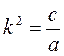— частота свободных колебаний, а .

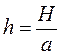Общий интеграл дифференциального уравнения (5.14), как известно, является суммой общего интеграла 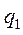соответствующего однород­ного уравнения, т. е. уравнения свободных колебаний, и какого-либо частного решения 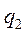уравнения (5.14): 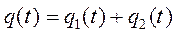, причем 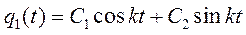. Частное решение 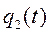ищем в виде: 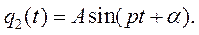Подстановка 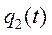в (5.14) приводит к соотношению 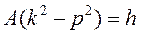, откуда при 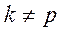находим .

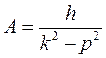Общий интеграл уравнения (3.63) будет:

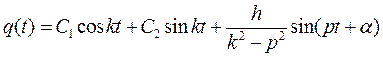
Правая часть этого равенства представляет результат наложения свободных колебаний на колебания, происходящие с частотой воз­мущающей силы и называемые вынужденными колебаниями. Если k>p, т. е. частота собственных колебаний больше частоты возму­щающей силы, то вынужденные колебания имеют ту же фазу, что и возмущающая сила; при k<p вынужденные колебания сдвинуты по фазе относительно возмущающей силы на π. Отметим, что амплитуда вынужденных колебаний не зави­сит от начальных условий движения. Зададимся вновь начальными усло­виями: 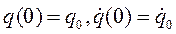при t=0 и пусть (для упрощения выкладок) α=0. Тогда постоянные интегрирования выразятся через начальные данные так: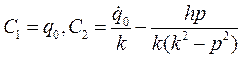

и решение уравнения (5.14) приведется к окончательному виду

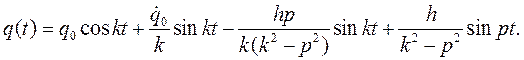(5.15)

Составное движение, представленное формулой (5.15), можно рассматривать как результат сложения: 1) свободных колебаний точки, которые возникли бы при отсутствии возмущающей силы, (первые два слагаемые), 2) колебаний, вызванных возмущающей силой, с собственной частотой k (третье слагаемое) и, наконец, 3) вынужденных колебаний с частотой возмущающей силы (последнее слагаемое). Если частота возмущающей силы р совпадает по величине с часто­той собственных колебаний k, то возникает явление резонанса. При резонансе возмущающая сила действует «в такт» с собственными колебаниями точки, что приводит к особенно интенсивному ее рас­качиванию. Амплитуда вынужденных колебаний при резонансе воз­растает, в чем можно убедиться следующим образом. Пусть начальные условия нулевые.

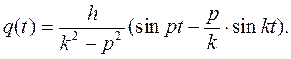(5.16)

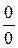Устремим р к k; тогда при p=k , имеем неопределенность вида . Раскрывая эту неопределенность по известному правилу Лопиталя, найдем:

Рис 61 В случае резонанса (p = k) движение системы определяется полученным выражением, содержащим в числе составляющих колебаний характерное для резо­нанса слагаемое 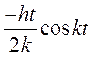в котором время t стоит множителем перед косинусом. Благодаря наличию этого множителя, 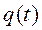, переходя от положи­тельных значений к отрицательным, будет вместе с тем неограни­ченно возрастать, колебания при резонансе происходят с возрастающей пропорционально времени ампли­тудой. График резонансного колеба­ния показан на рисунке 61. Явление резонанса, сопровождаю­щееся колебаниями весьма большой амплитуды, может служить причиной разрушения конструкции или создавать в ней опасные напряжения.

Точное совпадение частот собственных и вынужденных колебаний в технических приложениях практически невозможно (они могут совпадать с точностью измеряющих приборов). Поэтому рассмотрим случай, когда эти частоты очень близки. Будем считать

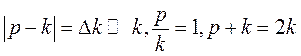(5.17)

Тогда формулу (5.16) можно переписать так

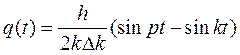
По известной формуле тригонометрии 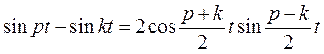, с учётом соотношений (5.17), перепишем полученную формулу в виде

.

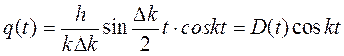Здесь D(t) –амплитуда колебаний системы с периодом колебаний 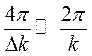. График полученных колебаний представлен на рисунке (62), здесь 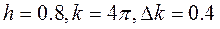. Такие колебания называются биениями системы, при стремлении 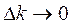получаем график резонансной кривой 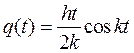(рис 61).

Рассмотрим пример, разобранный в этом параграфе, но добавим возмущающую гармоническую силу 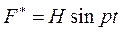, действующую на груз m. Для нахождения обобщённой силы составим выражение для элементарной работы

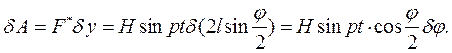
Рис 62

Обобщённая сила 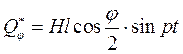зависит от обобщённой координаты φ, необходимо и здесь определить её значение для положения устойчивого равновесия, т.е. при φ=π/3. Дифференциальное уравнение вынужденных колебаний запишется в виде

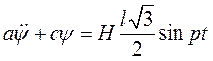или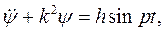

здесь

.

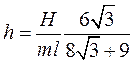Решение полученного дифференциального уравнения приведено выше.