Вынужденные колебания системы с учётом линейно-вязкого трения.

Для малых колебаний системы около устойчивого положения равновесия выражения для кинетической энергии, потенциальной энергии и диссипативной функции имеют вид;

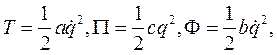
где 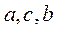-положительные постоянные. Будем предполагать, что обобщённая сила 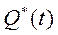является заданной функцией времени. Дифференциальное уравнение вынужденных колебаний будет линейным, неоднородным уравнением с постоянными коэффициентами

.

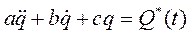При введённых ранее обозначениях 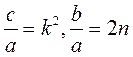оно примет вид

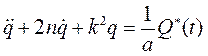(5.18)

Общий интеграл дифференциального уравнения (5.18), как известно, является суммой общего интеграла 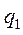соответствующего однород­ного уравнения, т. е. уравнения свободных колебаний, и какого-либо частного решения 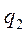уравнения (5.18): 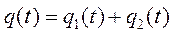, причем, в зависимости от значений коэффициентов n и k получим соответствующие решения. В случае произвольной функции 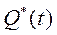решение ищется методом вариации произвольных постоянных. Здесь же ограничимся случаем, когда 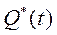гармоническая функция 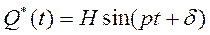. Уравнение (3.68) примет вид

,

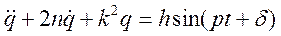где 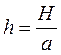. Будем искать частное решение в форме

.

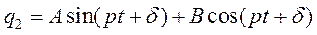Тогда

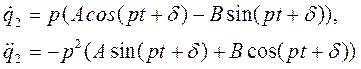
Подстановка в дифференциальное уравнение даёт

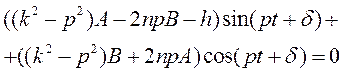
Откуда получаем два уравнении для неизвестных А и В:

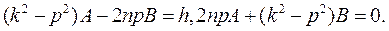
Решив эти уравнения, имеем:

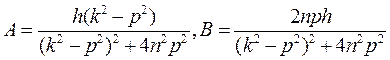
Полагая

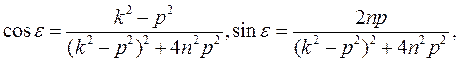
Получим 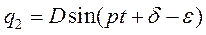, где

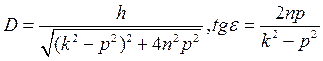. (5.16)

Общее решение можно теперь записать в таком виде

.

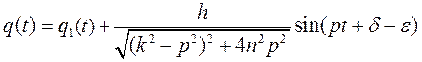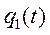- решение однородного уравнения в форме (5.11),(5.12) или (5.13), и, как было выше показано, оно при 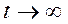затухает, остаются только вынужденные колебания. Поэтому в установившемся режиме 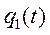можно не учитывать.