Уравнения статики деформируемого твёрдого тела.
§ 1. Дифференциальные уравнения равновесия нерастяжимой нити.
Задана невесомая нить длиной ds, (рис.65 ), нагруженная распределённой нагрузкой 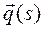 . Нить абсолютно гибкая и нерастяжимая. В данных предположениях достаточно записать уравнения равновесия в виде
. Нить абсолютно гибкая и нерастяжимая. В данных предположениях достаточно записать уравнения равновесия в виде 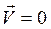 , главный вектор всех сил равен нулю.
, главный вектор всех сил равен нулю.

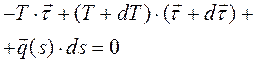
Раскроем полученное выражение
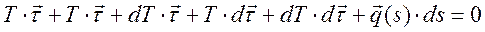 .
.
Первые два слагаемых сокращаются, произведением 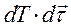 можно пренебречь, как величиной второго порядка, остаются только
можно пренебречь, как величиной второго порядка, остаются только 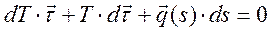 . Разделив полученную формулу на ds, получаем дифференциальное уравнение равновесия нити
. Разделив полученную формулу на ds, получаем дифференциальное уравнение равновесия нити
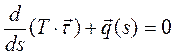 (6.1
(6.1
Или в проекциях на оси декартовой системы координат, вспоминая, что 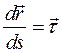 , имеем
, имеем
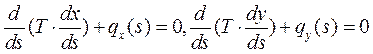 (6.2)
(6.2)
Уравнение (6.1) можно записать и в осях натурального триэдра, при этом
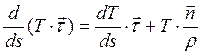
и окончательно получаем
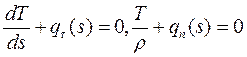 (6.3).
(6.3).
Рассмотрим приложения полученных двух формул: задачу о прогибе нити под действием своего веса и задачу о ленточном тормозе.
1. Равновесие цепи под действием своего веса (рис 66).
Цепь веса Р подвешена в двух точках на одном уровне. Расстояние между точками подвеса l. Считая прогиб цепи небольшим, определить прогиб и натяжение цепи. По определению
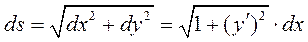
 Т.к. прогиб цепи небольшой, то можно считать
Т.к. прогиб цепи небольшой, то можно считать 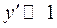 , тогда
, тогда 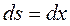 и уравнения (6.2) запишутся в виде:
и уравнения (6.2) запишутся в виде: 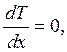 т.е.
т.е. 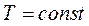 , а второе уравнение примет вид
, а второе уравнение примет вид 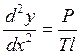 (здесь
(здесь 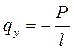 ). Интегрируя полученное выражение, получим уравнение параболы
). Интегрируя полученное выражение, получим уравнение параболы
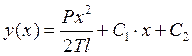 .
.
Для определения констант интегрирования зададим два граничных условия 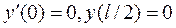 . Из первого условия
. Из первого условия 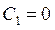 , а из второго
, а из второго 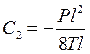 . Окончательно получаем
. Окончательно получаем
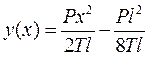
Максимальный прогиб будет при 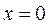 и равен
и равен 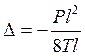 , отсюда можно получить значение натяжения цепи в зависимости от её прогиба,
, отсюда можно получить значение натяжения цепи в зависимости от её прогиба, 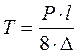 . В случае, если концы цепи находятся на разных уровнях, то в решение дифференциального уравнения надо подставить условия
. В случае, если концы цепи находятся на разных уровнях, то в решение дифференциального уравнения надо подставить условия 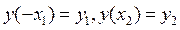 , где
, где 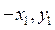 и
и 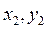 - координаты концов цепи.
- координаты концов цепи.
2. Задача о ленточном тормозе.
 На барабан радиуса R (на рис 67 показана часть барабана) находится нить АВ. К концам которой приложены две силы
На барабан радиуса R (на рис 67 показана часть барабана) находится нить АВ. К концам которой приложены две силы 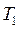 и
и 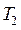 , причём пусть
, причём пусть 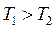 . Коэффициент трения скольжения между нитью и барабаном f. Надо определить: при каком соотношении
. Коэффициент трения скольжения между нитью и барабаном f. Надо определить: при каком соотношении 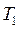 и
и 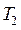 нить будет находиться в равновесии, т.е. не будет скользить по барабану. В нашем случае
нить будет находиться в равновесии, т.е. не будет скользить по барабану. В нашем случае 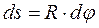 , а сила трения, направленная как показано на рис. , равна
, а сила трения, направленная как показано на рис. , равна 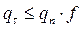 . Тогда из уравнений (6.3) имеем
. Тогда из уравнений (6.3) имеем 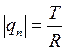 и
и 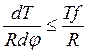 (*); это дифференциальное уравнение с разделяющимися переменными, интегрируя которое
(*); это дифференциальное уравнение с разделяющимися переменными, интегрируя которое 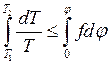 ,получим
,получим 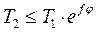 . Если
. Если 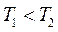 , то в уравнении (*) надо поменять знак
, то в уравнении (*) надо поменять знак 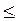 на
на 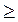 и порядок интегрирования по φ, тогда получим
и порядок интегрирования по φ, тогда получим 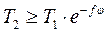 . Окончательно условие равновесия нити можно записать в виде
. Окончательно условие равновесия нити можно записать в виде
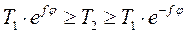
Дата добавления: 2016-01-07; просмотров: 1456;
