Теорема импульсов и её приложения в теории удара.

Явление удара тела о неподвижную преграду или соударения двух движущихся тел связано с процессом деформации тел вблизи точки их соприкасания и распространением волны сжатия внутри этих тел. Этот процесс не может быть изу
Рис 69 чен в рамках механики абсолютно твердого тела.
Предметом изучения теоретической механики служит лишь сравнение движения точки или системы точек до и после удара; при этом явление удара рассматривается как некоторый скачкообразный процесс, продолжительность которого бесконечно мала. На самом деле, продолжительность удара представляет хотя и очень малую, но конечную величину, зависящую от многочисленных физических факторов: упругих характеристик материала соударяющихся тел, их формы и размеров, относительной скорости сближения и др. В качестве примера укажем, что продолжительность соударения двух латунных шариков диаметра 26 мм при относительной скорости их сближения 74 мм/сек равна t = 2 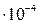 сек. Рассмотрим часто встречающийся случай, когда модуль F, возникающих при контакте сил изменяется по закону, изображенному на рис 69. До соударения модуль сил F равен нулю, затем растет, достигая некоторой максимальной величины, после чего быстро падает, обращаясь снова в нуль при t>τ. Импульс
сек. Рассмотрим часто встречающийся случай, когда модуль F, возникающих при контакте сил изменяется по закону, изображенному на рис 69. До соударения модуль сил F равен нулю, затем растет, достигая некоторой максимальной величины, после чего быстро падает, обращаясь снова в нуль при t>τ. Импульс 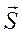 силы
силы 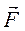 за время τ ее действия определяется обычной формулой
за время τ ее действия определяется обычной формулой
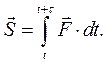
будем считать, что импульс силы при ударе конечен, хотя время действия импульса очень мало, а сила при этом очень большая. На основании теоремы об изменении количества движения имеем 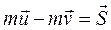 , или
, или 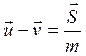 . Здесь
. Здесь 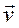 и
и 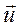 скорости точки в начале и конце удара. Так как импульс силы
скорости точки в начале и конце удара. Так как импульс силы 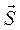 конечен, то при ударе скорость точки мгновенно изменяется на конечную величину. Найдём перемещение точки за время удара. Рассмотрим силу
конечен, то при ударе скорость точки мгновенно изменяется на конечную величину. Найдём перемещение точки за время удара. Рассмотрим силу 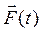 , изменяющуюся за время удара. Тогда
, изменяющуюся за время удара. Тогда 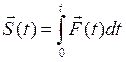 и
и
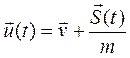 .
.
Интегрируя последнее равенство в пределах от нуля до τ , получим
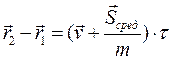 , (6.5)
, (6.5)
Где 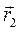 и
и 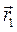 - радиусы – векторы точки в конечный и начальный моменты времени, а
- радиусы – векторы точки в конечный и начальный моменты времени, а 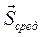 - среднее значение импульса
- среднее значение импульса 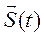 на отрезке (0, τ) . Из формулы (6.5) видно, что перемещение точки при мгновенном действии ударной силы
на отрезке (0, τ) . Из формулы (6.5) видно, что перемещение точки при мгновенном действии ударной силы 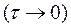 равно нулю.
равно нулю.
 Коэффициент восстановления. При соударении двух тел в точке контакта возникают ударные силы, приложенные к каждому из тел. Они имеют одинаковые модули и противоположно направлены. Пренебрегая трением, будем считать, что ударные силы и их импульсы
Коэффициент восстановления. При соударении двух тел в точке контакта возникают ударные силы, приложенные к каждому из тел. Они имеют одинаковые модули и противоположно направлены. Пренебрегая трением, будем считать, что ударные силы и их импульсы 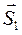 и
и 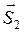 направлены по общей нормали к поверхностям
направлены по общей нормали к поверхностям
Рис 70 соударяющихся тел (см.рис 70 ). Как показывают наблюдения, гипотеза об абсолютной твердости тел является недостаточной для объяснения процесса удара и необходимо учитывать физические свойства тел. Сам процесс удара можно разбить на две фазы. В течение первой фазы происходит сближение тел по линии общей нормали, в результате чего проекция на нормаль относительной скорости точки контакта тел уменьшается до нуля. Вслед за этим начинается вторая фаза удара: тела, восстанавливая свою форму, начинают удаляться друг от друга, нормальная составляющая относительной скорости точки соприкосновения, переменив знак, возрастает по абсолютной величине, но не достигает, как правило, своего значения, в начале удара. Как показывают опыты, в первом приближении можно принять следующую гипотезу (гипотеза Ньютона): отношение модуля нормальной составляющей относительной скорости точки контакта тел после удара к ее величине до удара есть некоторая физическая постоянная, характеризующая физические свойства соударяемых тел, но не зависящая от их массы и относительной скорости. Эта физическая постоянная называется коэффициентом восстановления. Обозначая коэффициент восстановления через k и учитывая, что полного восстановления скорости, как правило, не происходит, будем иметь 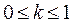 . В предельном случае, когда k = 1, удар называется абсолютно упругим, во втором предельном случае, когда k= 0, удар называется абсолютно неупругим. В остальных случаях (0<k<1) удар называется не вполне упругим, или просто упругим. Заметим, что при абсолютно неупругом ударе двух тел нормальная составляющая относительной скорости точки соприкосновения после удара равна нулю. Для таких тел весь процесс удара заключается только в первой фазе; после максимального сближения тел восстановления их формы в точке контакта не происходит, и оба тела движутся в дальнейшем совместно (в частности, оба тела могут остановиться) или одно тело скользит по поверхности другого.
. В предельном случае, когда k = 1, удар называется абсолютно упругим, во втором предельном случае, когда k= 0, удар называется абсолютно неупругим. В остальных случаях (0<k<1) удар называется не вполне упругим, или просто упругим. Заметим, что при абсолютно неупругом ударе двух тел нормальная составляющая относительной скорости точки соприкосновения после удара равна нулю. Для таких тел весь процесс удара заключается только в первой фазе; после максимального сближения тел восстановления их формы в точке контакта не происходит, и оба тела движутся в дальнейшем совместно (в частности, оба тела могут остановиться) или одно тело скользит по поверхности другого.
Обозначим через 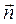 единичный вектор общей нормали к поверхностям тел в точке контакта, направленный внутрь второго тела. Пусть
единичный вектор общей нормали к поверхностям тел в точке контакта, направленный внутрь второго тела. Пусть 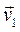 и
и 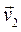 - скорости точек контакта первого и второго тел в начале удара, а
- скорости точек контакта первого и второго тел в начале удара, а 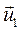 и
и 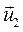 —соответствующие величины в конце удара. Тогда, по определению коэффициента восстановления, будем иметь
—соответствующие величины в конце удара. Тогда, по определению коэффициента восстановления, будем иметь
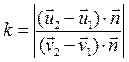
Коэффициент восстановления может быть определён следующим образом Представим себе, что одно из соударяемых тел выполнено в виде плиты и неподвижно закреплено в горизонтальном положении, другое тело— шарик. Шарик поднят на высоту 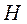 над плитой и отпущен без начальной скорости. Скорость его в момент соприкосновения с плитой вычисляется по известной формуле
над плитой и отпущен без начальной скорости. Скорость его в момент соприкосновения с плитой вычисляется по известной формуле 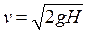 , измерив высоту h, на которую поднимается шарик после отскакивания, можно найти его скорость в конце удара:
, измерив высоту h, на которую поднимается шарик после отскакивания, можно найти его скорость в конце удара: 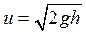 . Таким образом, коэффициент восстановления k оказывается равным
. Таким образом, коэффициент восстановления k оказывается равным 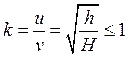 . Значения коэффициентов восстановления для различных пар соударяемых материалов приводятся в справочниках. Удар называется центральным, если центры масс соударяющихся тел находятся на общей нормали, проведённой в точке контакта.
. Значения коэффициентов восстановления для различных пар соударяемых материалов приводятся в справочниках. Удар называется центральным, если центры масс соударяющихся тел находятся на общей нормали, проведённой в точке контакта.  Рассмотрим косой удар точки о неподвижную преграду с учётом мгновенного трения, возникающего в точке контакта (рис. ). Запишем два отношения
Рассмотрим косой удар точки о неподвижную преграду с учётом мгновенного трения, возникающего в точке контакта (рис. ). Запишем два отношения
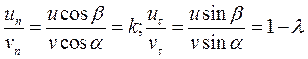 .
.
Первое – отношение нормальных составляющих скоростей после и до удара, второе – отношение касательных составляющих скоростей, где λ – коэффициент мгновенного трения. Разделив второе на первое, получим
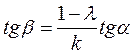 .
.
Скорость 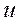 после удара равна
после удара равна
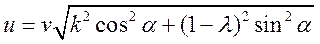
Дата добавления: 2016-01-07; просмотров: 1344;
