Общая постановка задачи обнаружения сигнала на фоне помех

Наблюдается процесс z(t), который может быть только помехой n(t) или результатом некоторого взаимодействия помехи n(t) и полезного сигнала x(t). Необходимо построить алгоритм, который позволил бы принять обоснованное решение о наличии или отсутствии сигнала в наблюдаемом процессе. В последствии этот алгоритм может быть реализован в виде программы обнаружения сигнала или в виде соответствующего технического устройства.

Поставленная задача в теории проверки статистических гипотез формализуется следующим образом:

- проверяется нулевая гипотеза 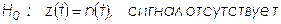против

- альтернативной гипотезы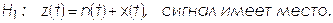

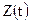Чаще всего оператору доступен только ограниченный отрезок одной единственной реализации сигнала , поэтому решении о принятии той или иной гипотезы приходится принимать по ограниченному числу опытных данных. В качестве таких данных используется выборка 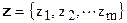, составленная из m отсчетов наблюдаемой реализации 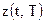, полученных после ее дискретизации и взятых в моменты времени 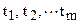, разделенных шагом дискретизации 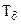. Выборку 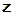можно рассматривать как случайный вектор с компонентами 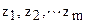или как случайную m – мерную величину. Полное статистическое описание случайного вектора дается плотностью совместного распределения его компонент 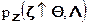, где:

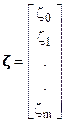- вектор возможных значений выборочных данных,[1]

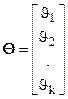- вектор параметров помех (мощность, границы частотного диапазона и т.д.),

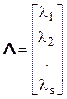- вектор параметров сигнала (амплитуда, частота, фаза и т.д.)

На практике помеху часто можно считать нормальным случайным процессом типа белого шума с единственным параметром 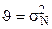, равным дисперсии помехи. Если передается синусоидальный сигнал, то вектор его параметров 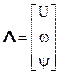включает в себя амплитуду сигнала, его частоту и начальную фазу.

В этом конкретном случае совместную плотность распределения компонент выборочного вектора можно записать в виде:

.

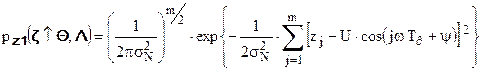В отсутствии сигнала 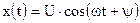, когда x(t)=0, совместная плотность распределения выборочного вектора принимает более простой вид:

.

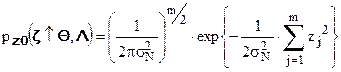Теперь задачу обнаружения сигнала можно сформулировать в терминах теории статистической проверки гипотез:

- гипотеза 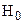заключается в том, что выборка подчиняется распределению ,

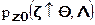- гипотеза 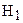заключается в том, что выборка подчиняется распределению .

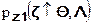Решение о соответствии той или иной гипотезы наблюдаемым данным принимается на основании некоторой решающей функции. Решающая функция алгоритма принятия решения разбивает пространство всех возможных выборок 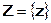на две непересекающихся област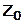и и 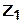, 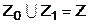и имеет вид:

.

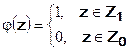В соответствии с решающей функцией при попадании вектора выборочных значений 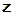в область 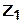принимается гипотеза 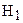(сигнал обнаружен), в другом случае принимается гипотеза 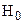(сигнала нет). Область 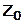считается допустимой (для принятия гипотезы об отсутствии сигнала), область 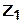называется критической областью.

Вся проблема заключается теперь в подходящем выборе допустимой и критической областей. Задача их определения и есть задача построения оптимального алгоритма обнаружения сигнала. Для определения этих областей предварительно следует дать формулировку оптимальности алгоритма.

В силу ограниченности и случайности наблюдаемых данных возможны ошибки при принятии решений.

Ошибка первого рода (ложная тревога) заключается в том, что принимается решение об обнаружении сигнала, когда его на самом деле нет. Вероятность ошибки первого рода составляет:

,

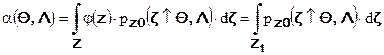и зависит от параметров шума и ожидаемого сигнала.

Ошибка второго рода (пропуск перехода) заключается в том, что принимается гипотеза об отсутствии сигнала, хотя он имеет место. Это ошибка того, что наблюдатель не смог обнаружить появление сигнала. Вероятность появления ошибки второго рода составляет:

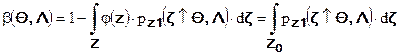
и также зависит от параметров шума и не обнаруженного сигнала.

Вероятность правильного обнаружения сигнала, дополняющая вероятность ошибки второго рода до единицы, рассматриваемая в функции параметров сигнала и шума, называется мощностью или функцией мощности алгоритма принятия решения:

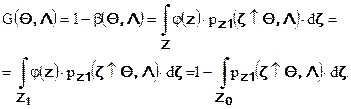
Вероятность правильного принятия гипотезы об отсутствии сигнала дополняет до единицы вероятность ошибки первого рода. В функции параметров шума и сигнала эта вероятность называется оперативной характеристикой алгоритма принятия решения:

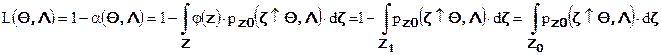Для уменьшения вероятности ошибки первого рода следует уменьшать размер критической области 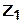, но при этом расширяется допустимая область 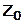и поэтому возрастает вероятность ошибки второго рода. В результате возникает необходимость поиска компромисса – приемлемого или допустимого сочетания вероятностей ошибок первого и второго рода.