Частотная фильтрация.

Предположим, что передаваемый кодированный сигнал имеет форму отрезков синусоиды:

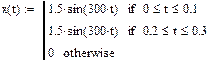
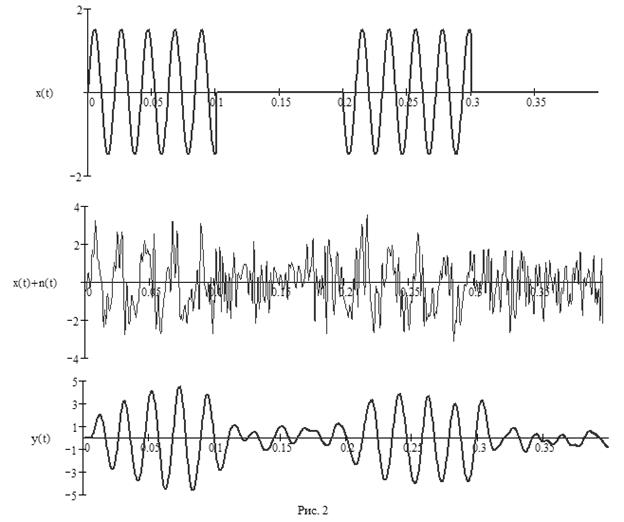
На рис. 2 сверху представлен отрезок сигнала x(t), а в середине – тот же сигнал, но в смеси с белым шумом n(t). Здесь нужно иметь большое воображение, чтобы заметить следы сигнала x(t) на фоне шума.

Для выделения сигнала естественно использовать полосовой фильтр с узкой полосой пропускания, средняя частота которого равна частоте сигнала .

На рис. 2 внизу представлен сигнал y(t) на выходе резонансного фильтра, настроенного на частоту сигнала x(t) при степени успокоения 0,2. Дифференциальное уравнение фильтра и порядок его решения в среде Math Cad представлено в листинге:

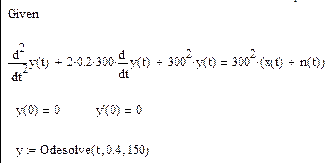
На графике (рис. 2) уже можно четко заметить полезный сигнал, несмотря на имеющие место искажения остатками шума.

Пусть n(t) – белый широкополосный шум с мощностью 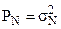в полосе частот до 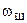. В этом случае мощность шума на выходе фильтра с полосой пропускания 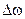вокруг частоты 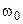составит:

.

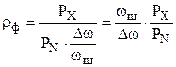Казалось бы, что, уменьшая полосу пропускания фильтра по отношению к полосе частот, занимаемых шумом, можно как угодно увеличивать отношение сигнал/шум и тем самым все более четко определять наличие сигнала на фоне шума.

Однако здесь следует иметь в виду следующее обстоятельство. Спектр синусоидального сигнала сосредоточен на его частоте только в том случае, когда эта синусоида задана на всем промежутке времени от 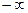до .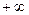

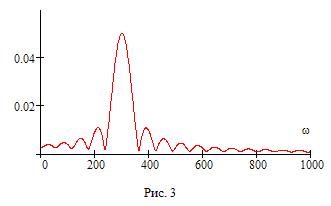
Отрезок синусоиды конечной протяженности имеет лепестковый спектр (рис. 3), главный максимум которого приходится на частоту сигнала 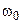. Полосовой фильтр обязательно поглощает часть энергии полезного сигнала вместе с энергией шума, что приводит к амплитудным и фазовым искажениям сигнала. Это хорошо видно на нижнем графике, на рис. 2.