Амплитудно-частотная характеристика

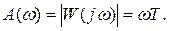(6.5)

Ее график есть прямая линия, наклон которой к оси частот тем больше, чем больше величина постоянной времени (рис.6.1). Из рис.6.1следует, что дифференцирующее звено является фильтром высоких частот, так как амплитуда выходного сигнала растет с увели­чением частоты входного сигнала.

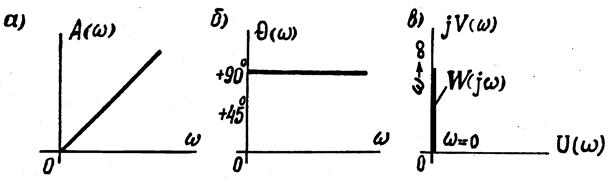
Рис. 6.1 Частотные характеристики дифференцирующего звена

Фазовая частотная характеристика

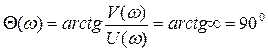(6.6)

показана на рис.6.1,б. Это означает, что дифференцирующее звено на всех частотах создает опережение по фазе выходного сигнала по отношению к входному на 90°.

Логарифмические амплитудная и фазовая частотные характеристики (рис.6.2) определяются выражениями:

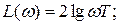(6.7)

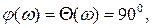(6.8)

из которых следует, что они являются зеркальными отображениями характеристик L(ω) и L(ω) интегрирующего звена (см. рис.6.2).

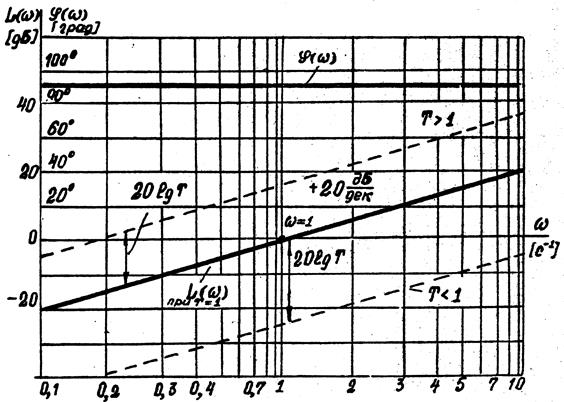
Рис.6.2. Логарифмические частотные характеристики

дифференцирующего звена

Иными словами, они имеют одинаковую форму, но отличаются знаком. Характеристика L(ω) при Т = 1 с проходит через точку ω=1 с^-1 снаклоном +20 дБ/дек. При Т ≠ 1 с график смещается вверх или вниз на величину +20lg Т (рис.6.2), пересекая ось частот в точке ω=1/ Т.

Необходимо отметить, что передаточная функция дифференцирую­щего звена W(р)=Тр, иногда называемого идеальным дифференци­рующим звеном, точно не может быть реализована. Однако многие ре­альные элементы по своим динамическим свойствам близки к дифферен­цирующему звену, т.е. их характеристики при определенных условиях (например, частотные характеристики в некотором диапазоне частот) одинаковы. Примером таких элементов является тахогенератор постоян­ного тока (рис.6.3,а), напряжение U_вых на обмотке якоря которого пропорционально угловой скорости вращения якоря Ω. Так, как 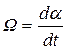где α - угол поворота якоря, то 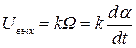. Здесь k - передаточный коэффициент, имеющий размерность В·с/рад или В·с/град.

К дифференцирующим звеньям можно также отнести дифференци­рующий трансформатор, электрические емкостно-омический (рис.6.3,б) и индуктивно-омический дифференцирующие контуры постоянного тока, нашедшие широкое применение в различных отраслях техники.

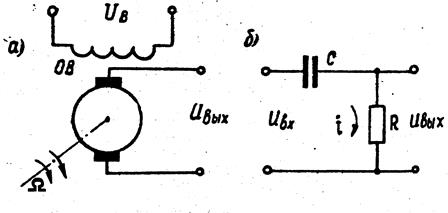
Рис. 6.3. Примеры дифференцирующих звеньев

В качестве примера рассмотрим дифференцирующий RС-контур (рис.6.3,б), уравнение и передаточная функция которого имеют вид:

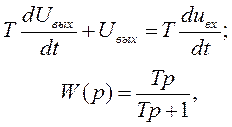
т.е. отличаются от уравнения (6.2) и функции (6.3). Следует помнить, что чем меньше постоянная времени контура Т, тем точнее выполняется дифференцирование.

2.Форсирующее звено первого порядка.

Форсирующим звеном первого по­рядка называется звено, уравнение которого имеет вид 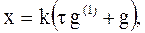(6.9)

или может быть приведено к такому виду.

Здесь 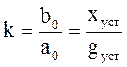- передаточный коэффициент, характеризующий стати-ческие свойства звена;

x_уст и g_уст - установившиеся значения выходной и входной величин;

τ=b₁/b₀ - постоянная временя, характеризующая степень влияния скорости изменения входной величины на выходную величину,

a₀, b₀, b₁- коэффициенты уравнения звена, записанного в нестандартной форме

a₀x= b₁g⁽¹⁾+ b₀g.