Фазовая частотная характеристика звена
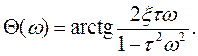 (6.21)
(6.21)
Пользуясь выражением (6.19) и изменяя частоты ω от 0 до ∞, построим амплитудно-фазовую характеристику звена, изображенную на рис.6.7, в. Эта характеристика представляет собой параболу, расположенную в верхней полуплоскости, которая начинается из точки k при ω=0, проходит через точку 2kξ при 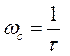 , уходит в бесконечность при ω→∞.
, уходит в бесконечность при ω→∞.
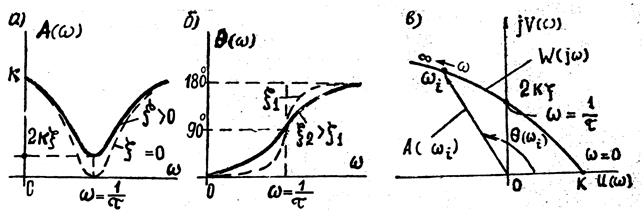
Рис.6.7. Частотные характеристики форсирующего звена
второго порядка
Пользуясь выражениями (6.20) и (6.21), можно построить амплитудную и фазовую частотные характеристики. Графики этих характеристик приведены соответственно на рис.6.7, а, б. Из анализа выражения (6.21) и рис.6.7, б следует, что звено создает опережение по фазе, которое тем больше, чем больше частота ω. При 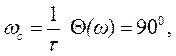 при
при 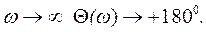
Следовательно, фазовая частотная характеристика изменяется от 0 до +180°, причем, чем меньше величина ξ,тем резче изгиб характеристики около точки 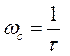 .Из рассмотрения рис.6.7., а и выражения (6.2) следует, что звено является фильтром высоких частот. Амплитудная частотная характеристика при ω=0 начинается из точки k на оси абсцисс, имеет значение, равное 2kξ при
.Из рассмотрения рис.6.7., а и выражения (6.2) следует, что звено является фильтром высоких частот. Амплитудная частотная характеристика при ω=0 начинается из точки k на оси абсцисс, имеет значение, равное 2kξ при 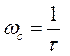 , и неограниченно возрастает при ω→∞..
, и неограниченно возрастает при ω→∞..
Логарифмические частотные характеристики звена:
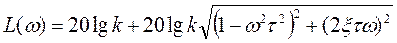 (6.22)
(6.22)
и
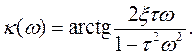 (6.23)
(6.23)
являются зеркальным отображением логарифмических частотных характеристик L(ω) и φ(ω) колебательного звена относительно оси частот. Для построения логарифмических частотных характеристик звена могут быть использованы шаблоны, изготовленные для различных значений ξ. Характеристика L(ω) форсирующего звена второго порядка при ξ=0 терпит разрыв, выражение (6.22) позволяет построить точную ЛАЧХ звена. Приближенно эта характеристика может быть заменена асимптотической характеристикой, т.е. ломаной, образованной из отрезков асимптот:
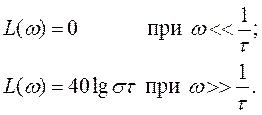
если k =1. При k ≠1эта характеристика смещается на величину 20 lgk вверх при k>1 и вниз при k<1. В диапазоне частот 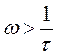 характеристика имеет наклон +40 дБ/дек (рис.6.8, а).
характеристика имеет наклон +40 дБ/дек (рис.6.8, а).
Вид логарифмической фазовой частотной характеристики звена для нескольких значений ξ показан на рис.6.8, б.
Примером реального форсирующего звена второго порядка может служить схема, изображенная на рис.6.9, которая получена путем последовательного соединения двух емкостно-омических форсирующих контуров первого порядка.
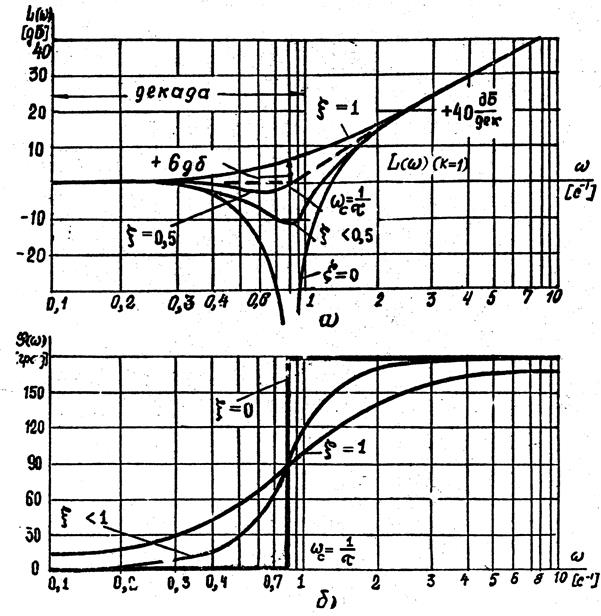
Рис.6.8. Логарифмические частотные характеристики
форсирующего звена второго порядка
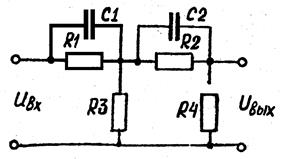
Рис.6.9. Примеры форсирующего звена второго порядка
Уравнение данного звена имеет следующий вид:
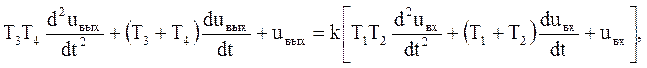
где
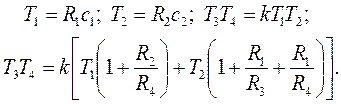
Передаточная функция этой схемы имеет вид:
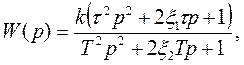
где 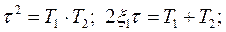
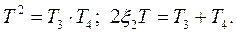
Если выбрать параметры схемы так, чтобы постоянные времени Т3 и Т4 были малы, то ее динамические свойства будут близки к свойствам форсирующего звена второго порядка.
Дата добавления: 2015-12-11; просмотров: 1245;
