Фазовая частотная характеристика
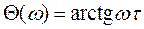(6.13)
также является возрастающей функцией (рис.6.4, б). Форсирующее звено создает опережение по фазе, которое изменяется от 00 при ω=0 до 900 при ω→∞. При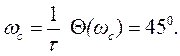 
На рис.6.4, а, б показаны частотные характеристики звена при двух значениях постоянной времени.
Логарифмические частотные характеристики форсирующего звена первого порядка:
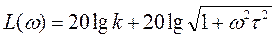(6.14)
и
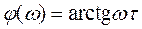(6.15)
отличаются лишь знаком от логарифмических частотных характеристик апериодического звена. Поэтому они могут быть построены путем зеркального отображения характеристик L(ω) и φ(ω) апериодического звена относительно оси частот (рис.6.5)
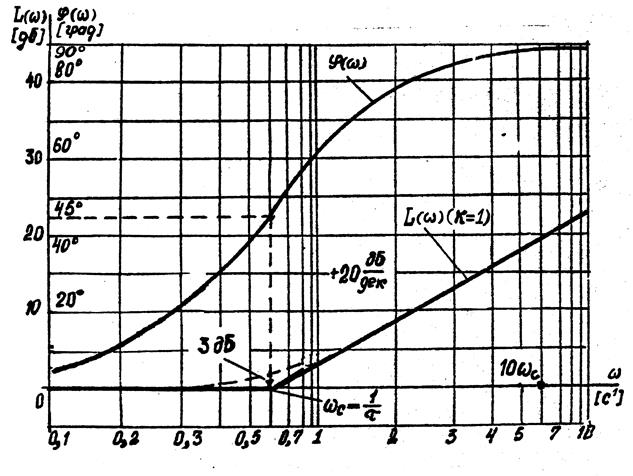
Рис.6.5. Логарифмические частотные характеристики форсирующего звена
первого порядка
Точная ЛАЧХ (показана пунктиром на рис.6.5) отличается от приближенной, или асимптотической (показана сплошной линией), при сопрягающей частоте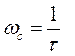 
на величину
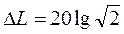
При k =1 L(ωс)≈3 дБ. Нетрудно показать, что наклон логарифмической амплитудной частотной характеристики при ω>ωс равен +20 дБ/дек.
Примером форсирующего звена первого порядка является электрический RC-контур, схема которого приведена на рис.6.6. Передаточная функция такого контура
(6.16)
где постоянные времени τ, Т и передаточный коэффициент k определяются следующими выражениями:
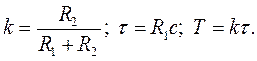
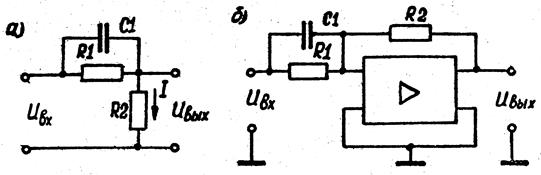
Рис.6.6. Примеры форсирующего звена
первого порядка
Следовательно, данный контур эквивалентен цепочке из двух последовательно соединенных звеньев: форсирующего звена первого порядка с передаточной функцией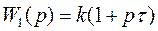 
и апериодического с передаточной функцией 
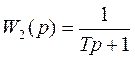. Если параметры этих контуров R1, R2 и c подобрать так, что постоянная времени Т будет малой, то приближенно можно записать: 
. Таким образом, получим передаточную функцию форсирующего звена первого порядка.
2.Форсирующее звено второго порядка.
Уравнение этого звена имеет вид
(6.17)
причем коэффициент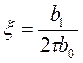 
должен быть меньше единицы. В приведенном уравнении:
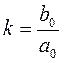- передаточный коэффициент звена;
- постоянная времени звена;
a0, b0, b1, b2 - коэффициенты уравнения звена, записанного в нестандартной форме:
a0x=b2 g(2)+ b1 g(1)+b0 g.
При ξ≥1 рассматриваемое звено будет эквивалентно двум последовательно соединенным форсирующим звеньям первого порядка.
Передаточная функция звена
W(p)=k(τ2p2+2ξτp+1). (6.18)
Полагая p=jω, получим комплексную передаточную функцию вида
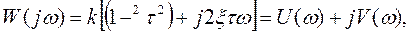(6.19)
где U(ω)=k(1-τ2ω2) – вещественная частотная характеристика;
V (ω)=2kξωτ – мнимая частотная характеристика.
Амплитудно-частотная характеристика звена
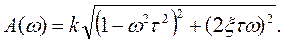(6.20)
Дата добавления: 2015-12-11; просмотров: 994;