Комплексная частотная характеристика согласованного фильтра

Комплексная частотная характеристика согласованного фильтра может быть найдена как преобразование Фурье от h_opt(t), определяемой выражением (6.20)

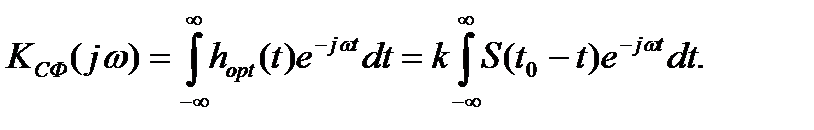
Сделав замену переменных 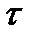=t₀-t, получим

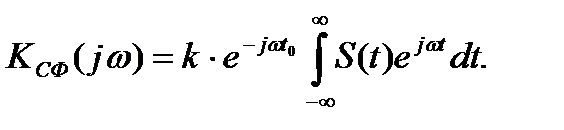(6.24)

Интеграл в формуле (6.24) определяет комплексно-сопряжённый спектр сигнала

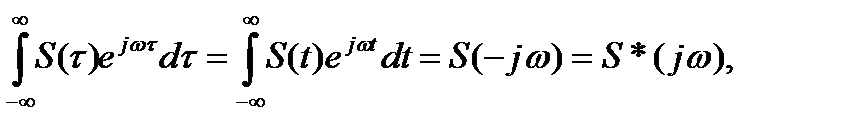(6.25)

так как в показателе экспоненты стоит знак плюс, а не минус, как это надо для определения спектра сигнала.

Таким образом, комплексная частотная характеристика согласо­ванного фильтра

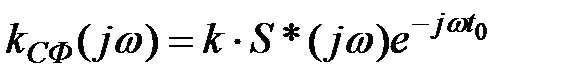(6.26)

пропорциональна произведению комплексно-сопряженного спектра сигнала S*( 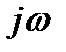) на множитель задержки 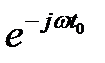Представим комплексный спектр S( 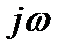) сигнала S(t) в виде

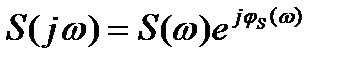, (6.27)

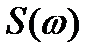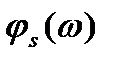где и - соответственно амплитудный и фазовый спектры сигнала.

Комплексно-сопряженный спектр будет отличаться от (6.27) только знаком показателя экспоненты:

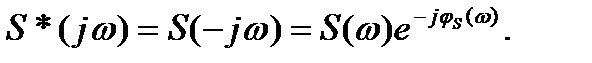(6.28)

Подставив (6.28) в (6.26), получим

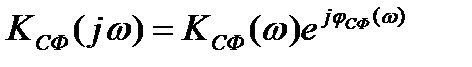(6.29)

где К_сф( 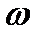) = k ×S( 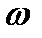) - амплитудно-частотная характеристика (АЧХ) согласованного фильтра,

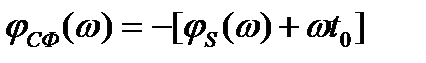- фазочастотная характеристика (ФЧХ) согласованного фильтра.

Пропорциональность АЧХ согласованного фильтра амплитудному спектру сигнала приводит к тому (рис.6.4), что коэффициенты передачи фильтра больше на тех частотах, на которых выше амплитуда спектральных составляющих сигнала, и меньше там, где составляющая ниже.

ФЧХ согласованного фильтра определяется взятой с обратным знаком суммой фазового спектра сигнала 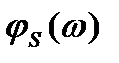и пропорционального частоте 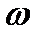угла задержки 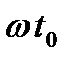. Возьмём одну гармоническую составляющую спектра сигнала на произвольной частоте 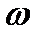, имеющую (для простоты изложения) конечную амплитуду S( ):

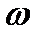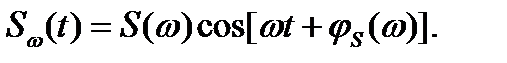
Эта составляющая, пройдя через фильтр, увеличит свою амплитуду в - 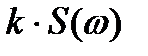раз и получит фазовую задержку, равную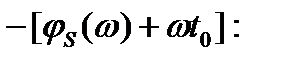

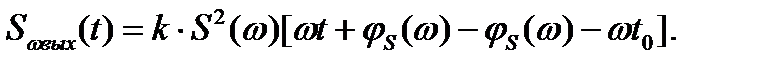
В момент t = t₀ гармоническая составляющая будет равна своей амплитуде

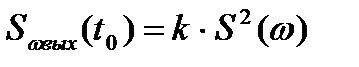. (6.30)

Рис. 6.4

Так как частота составляющей 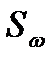(t) была выбрана произвольно, то можно сделать следующий вывод: на выходе согласованного фильт­ра в момент t = t₀ все гармонические составляющие равны своим амплитудным составляющим. Благодаря этому выходной сигнал S_вых(t) в момент времени t=t₀ формируется в результате арифметического сложения всех амплитуд гармонических составляющих выходного спектра.

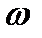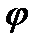Таким образом К_сф( ) и _сф( 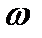) подобраны так, чтобы обеспечить максимум пика выходного сигнала при t= t₀. и в соответствии с этим получить наибольшее отношение сигнал/шум. При этом форма выходного сигнала не будет совпадать с формой входного сигнала. Более того, искажение формы здесь принципиально необходимо, чтобы получить наибольшее пиковое отношение сигнал/шум на выходе. Кроме того, заметим, что все характеристики согласованного фильтра, например h_сф(t) и К_сф( 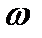), при белом шуме на входе полностью определяются характеристиками сигнала S(t), Момент t₀ совпадает с длительностью импульсного сигнала, если импульс одиночный, или с длительностью пачки импульсов, если сигнал представляется в виде нескольких импульсов, образующих пачку.