Критерии оптимального обнаружения и различения сигналов
Критерием оптимальности называется правило, по которому из всех возможных обнаружителей можно выбрать наилучший.
Наиболее общим критерием оптимального обнаружения является критерий Байеса, или иначе - критерий минимума среднего риска.
С точки зрения критерия Байеса оптимальным считается такой обнаружитель, который имеет минимальную вероятность ошибочных решений с учетом их «веса» или степени нежелательности.
Используя условные вероятности Рпо , Рлт и выражение (7.3), можно записать следующее выражение для среднего риска процесса обнаружения
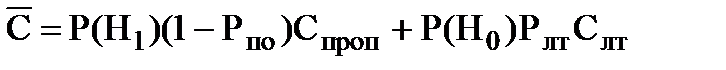 , (7.4)
, (7.4)
где Спроп и Слт - веса ошибочных решений.
Вынесем в выражении (7.4) за скобки Р(Н1)Спроп , тогда
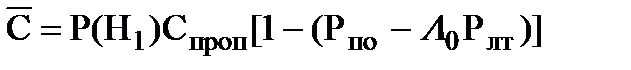 , (7.5)
, (7.5)
где L0 - весовой множитель, равный
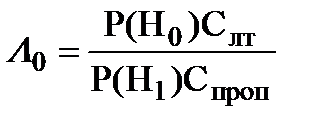 .
.
Из анализа (7.5) следует, что условие минимизации 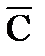 заключается в получении максимального значения разности (Рпо - L0Рлт ), которую называют взвешенной разностью.
заключается в получении максимального значения разности (Рпо - L0Рлт ), которую называют взвешенной разностью.
Таким образом,
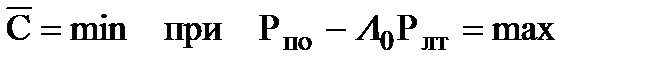 . (7.6)
. (7.6)
Критерий Байеса является наиболее общим. На его основе, как частные случаи, могут быть получены и другие критерии.
Если принять веса ошибок одинаковыми Спроп = Слт = 1, то из (7.4) получим, что средний риск равен суммарной вероятности ошибки
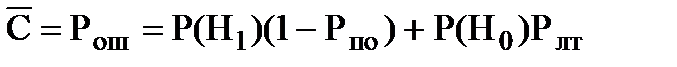 . (7.7)
. (7.7)
Условие минимума суммарной вероятности ошибки (7.7) называется критерием идеального наблюдателя. Он используется при решении задач передачи сообщений, где одинаково нежелательны как пропуски, так и искажения элементов сообщения.
По аналогии с (7.6) для критерия идеального наблюдателя можно записать вместо (7.7) следующее условие оптимизации
 . (7.8)
. (7.8)
В радиолокации наибольшее применение находит критерий Неймана-Пирсона, являющийся частным случаем критериев Байеса и идеального наблюдателя. Сущность критерия заключается в том, что фиксируется условная вероятность ложной тревоги Рлт , после чего максимизируется условная вероятность правильного обнаружения Рпо .
Критерий записывается в виде
Рлт = const , Рпо = max , (7.9)
Широкое применение критерия Неймана-Пирсона в радиолокации объясняется тем, что:
во-первых, как правило, неизвестны априорные вероятности Р(Н0) и Р(Н1), а также Спроп и Слт ;
во-вторых, в обзорных РЛС большую часть интервала наблюдения принятый сигнал обусловлен только шумом, поэтому ложная тревога является крайне нежелательной и ее величина должна быть ограничена заранее, исходя из тактических соображений. Обычно задают Рлт = 10-10 …10-6 , используя выражение Рлт » tш / Тлт ; где tш - длительность шумового выброса, Тлт - период появления ложной тревоги.
Таким образом, в результате наблюдения выборки (x1 ,..., xn ) по выбранному критерию оптимальности должно быть получено одно из двух взаимоисключающих решений: А- сигнал есть, 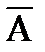 - сигнала нет. Каждая возможная выборка представляется в многомерном пространстве одной точкой. Оптимальный обнаружитель должен разделить пространство выборок на два соприкасающихся пространства X и
- сигнала нет. Каждая возможная выборка представляется в многомерном пространстве одной точкой. Оптимальный обнаружитель должен разделить пространство выборок на два соприкасающихся пространства X и 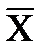 .Если точка М, соответствующая k-й выборке (x1 ,..., xn), попадает в пространство X - принимается решение А, в противном случае - решение
.Если точка М, соответствующая k-й выборке (x1 ,..., xn), попадает в пространство X - принимается решение А, в противном случае - решение 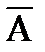 . В соответствии с критерием (7.6) можно записать
. В соответствии с критерием (7.6) можно записать
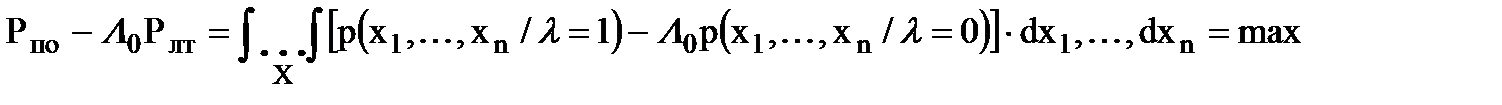 , (7.10)
, (7.10)
где р(x1 , ..., xn / l = 1) и p(x1 , ..., xn / l =0) - условные n-мерные плотности вероятности дискретной выборки (x1 , ..., xn ) при наличии сигнала (l = 1) и при его отсутствии (l = 0) соответственно.
Выполнение условия (7.10) возможно при положительной подынтегральной разности
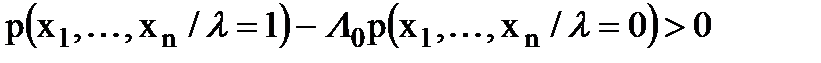 ,
,
то есть
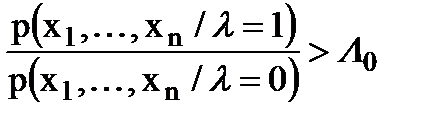 . (7.11)
. (7.11)
Следовательно, оптимальный обнаружитель должен вычислять величину
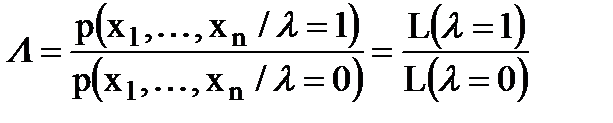 , (7.12)
, (7.12)
определяемую отношением функций правдоподобия L(l = 1) и L(l = 0) и называемую отношением правдоподобия. Если L сравнить с некоторым порогом L0 , то получим правило принятия решения
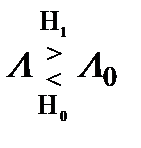 . (7.13)
. (7.13)
Таким образом, критерием оптимального обнаружения может служить критерий отношения правдоподобия, являющийся следствием общего критерия Байеса. В соответствии с этим критерием оптимальный обнаружитель (рис.7.2) должен сформировать отношение правдоподобия (блок ОП) и подать его на пороговое устройство ПУ, где осуществляется процедура сравнения L с порогом L0 , в результате которой выносится одно из двух возможных решений: 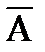 - нет сигнала или А - есть сигнал. Выбор какого-то частного критерия оптимальности (байесовского, идеального наблюдателя, Неймана - Пирсона) сказывается лишь на значении порога L0 , никак не влияя на основную часть обнаружителя - блок ОП, где происходит оптимальная обработка реализации x(t). В радиолокации значение порога L0 устанавливается исходя из критерия Неймана-Пирсона.
- нет сигнала или А - есть сигнал. Выбор какого-то частного критерия оптимальности (байесовского, идеального наблюдателя, Неймана - Пирсона) сказывается лишь на значении порога L0 , никак не влияя на основную часть обнаружителя - блок ОП, где происходит оптимальная обработка реализации x(t). В радиолокации значение порога L0 устанавливается исходя из критерия Неймана-Пирсона.
| ОП |
| ПУ |
| x(t) |
| L0 |
| L |
| A |
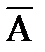
|
Рис. 7.2.
Дата добавления: 2016-01-26; просмотров: 5734;
