На фоне белого шума. Структурные схемы обнаружителей

Рассмотрим задачу синтеза оптимального обнаружителя сигнала с полностью известными параметрами на фоне белого шума. Наблюдаемый процесс x(t) = l×s(t) + n(t) , l = 0,1 , 0£ t £T является либо аддитивной смесью сигнала и шума (при l =1), либо одним шумом (при l =0), время наблюдения Т фиксировано. Вначале рассмотрим случай, когда наблюдение ведется в дискретные моменты времени t₁ ,..., t_n , при этом принимаются выборочные значения x(t_k) = x_k = ls_k + n_k , l = 0,1; k =1,2,...,n. Оптимальный обнаружитель должен формировать отношение правдоподобия

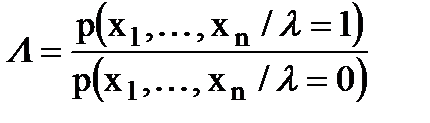
и сравнивать его с порогом L₀ . Чтобы определить структуру устройства, формирующего отношение правдоподобия, необходимо конкретизировать плотности вероятности, входящие в (7.12).

Поскольку рассматриваемый белый шум описывается гауссовской плотностью вероятности, то

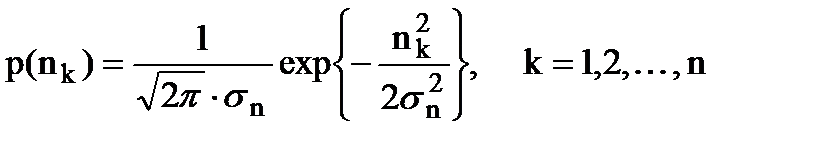. (7.14)

Учитывая, что выборки белого шума статистически независимы, а также то, что x_k º n_k при l = 0, имеем

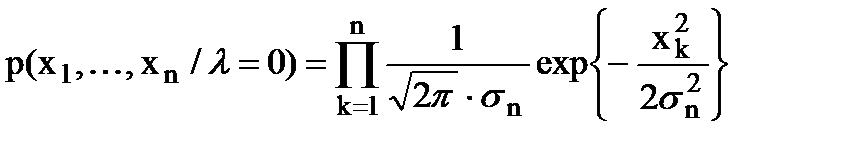. (7.15)

Так как сигнал является детерминированным, то распределение вероятностей выборки (x₁, ... , x_n ) при l = 1 остается гауссовским, однако средние значения отсчетов теперь не равны нулю, при этом

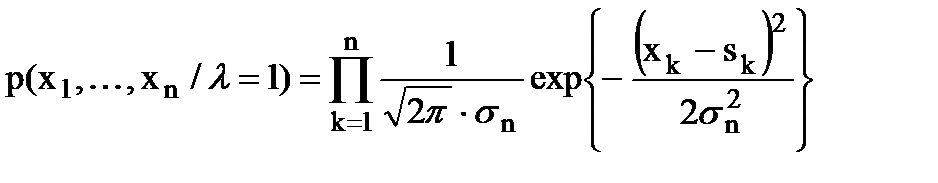. (7.16)

Подставив (7.15) и (7.16) в (7.12), получим

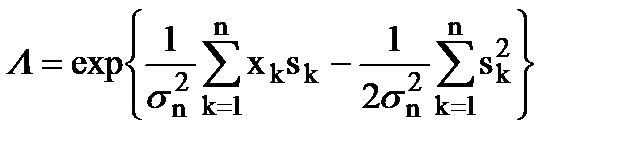. (7.17)

Для упрощения обработки целесообразно вместо отношения правдоподобия L формировать его логарифм

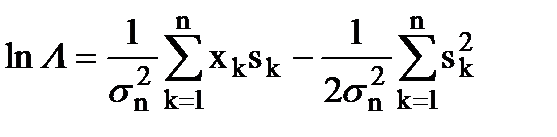. (7.18)

Перейдем к непрерывному времени наблюдения. Положим t₁ =0, t_n = T, кроме того, учтем, что плотность вероятности независимых гауссовских величин (7.15) при непрерывном времени наблюдения переходит в функционал плотности вероятности белого шума. Если спектральная плотности последнего равна N₀/2 , а 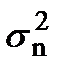- дисперсия гауссовских величин n_k , то при переходе к непрерывному времени (от n_k к n(t)) можно воспользоваться зависимостью

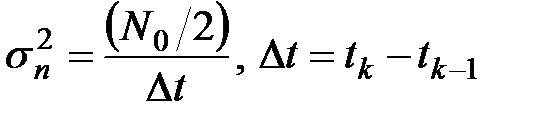(7.19)

(при Dt ® 0 , 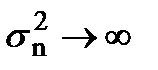). Подставляя (7.19) в (7.18) и переходя к пределу при Dt ® 0, получим

.

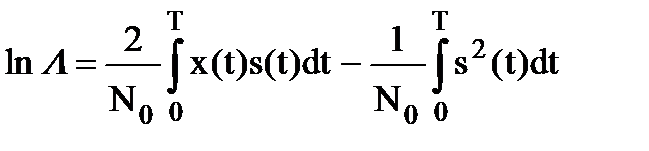При этом правило принятия решения можно записать в следующем виде

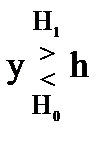, (7.20)

где

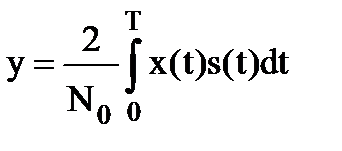, (7.21)

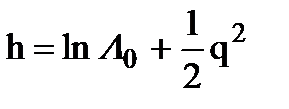. (7.22)

Выражение (7.21) определяет достаточную статистику y, являющуюся взаимным корреляционным интегралом между наблюдаемым процессом x(t) и копией сигнала s(t).

Выражение (7.22) определяет порог h, зависящий от L₀ и отношения сигнал /шум, квадрат которого равен

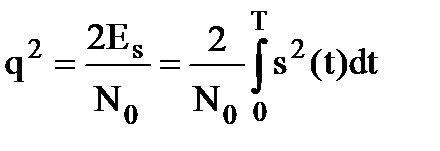. (7.23)

Формулы (7.20), (7.21), (7.22) позволяют построить структурную схему оптимального обнаружителя в виде корреляционного приемника с пороговым устройством (рис. 7.3).

Рис. 7.3

На умножитель подается принимаемый процесс x(t) и опорный сигнал s(t), являющийся точной копией обнаруживаемого (ожидаемого) сигнала. Интегрирование произведения x(t)s(t) в течение Т дает корреляционный интеграл y. В пороговом устройстве (ПУ) производится сравнение значения корреляционного интеграла в момент ожидаемого окончания действия сигнала Т с порогом h и принимается решение о наличии или отсутствии сигнала. Начало интегрирования и его окончание совпадают по времени с началом и окончанием ожидаемого сигнала s(t), что обеспечивается устройством синхронизации (УС). Это же устройство синхронизирует работу генератора опорного сигнала (ГОС) для коррелятора.

Техническая реализация оптимального обнаружителя в виде корреляционного приемника не является единственно возможной. Корреляционный интеграл может быть сформирован также при помощи согласованного фильтра. Его импульсная характеристика согласована с обнаруживаемым сигналом, являясь в соответствии с выражением

h_сф(t) = k×s(T - t) (7.24)

“зеркальным отражением” формы сигнала (рис.7.4).

Поскольку согласованный фильтр - составная часть оптимального обнаружителя (см. рис.7.5) и максимизирует отношение сигнал/шум на выходе, его называют также оптимальным. Максимальное отношение сигнал/шум по мощности на выходе СФ достигается в момент времени Т и составляет величину

q_сф = 2Е_s / N₀ . (7.25)

Ни один из линейных фильтров не может дать отношение сигнал/шум больше, чем согласованный фильтр (либо коррелятор). Как следует из рис.7.5, для согласованного фильтра отпадает необходимость в обеспечении синхронизации между опорным и принимаемым сигналами с точностью до фазы их высокочастотного заполнения. Это является достоинством СФ по сравнению с коррелятором.

Рис.7.4 Рис.7.5