Обнаружение сигнала со случайными начальной фазой и амплитудой

На практике обычно неизвестна не только начальная фаза радиосигнала, но и его амплитуда. В этом случае используется модель сигнала со случайными начальной фазой и амплитудой

s(t, a, j) = aU(t)cos(w₀t + y(t) - j), (8.16)

где безразмерный параметр а, определяющий амплитуду сигнала, полагается случайной величиной, распределенной по закону Релея (при условии, что радиолокационный объект можно представить в виде большого числа статистически независимых случайных отражателей)

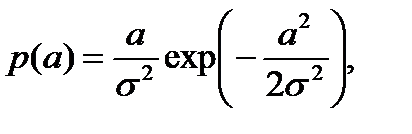(8.17)

а фаза j - по равномерному закону (8.9).

Учитывая, что случайные величины a и j статистически независимы, отношение правдоподобия для рассматриваемого случая по аналогии с (8.10) можно представить в виде

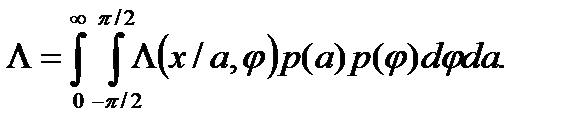
Подставляя сюда (8.9) и выражение для условного отношения правдоподобия L(х/a,j) (которое получается из (8.17) путем замены s(t) на s(t, a, j)) и интегрируя затем по j, находим

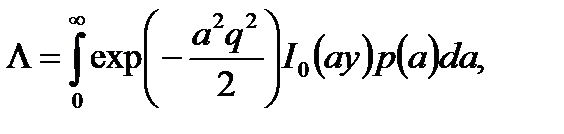
где q² = 2E_s /N₀, E_s - энергия сигнала, соответствующая значению а = 1. Далее, используя (8.17) и интеграл

,

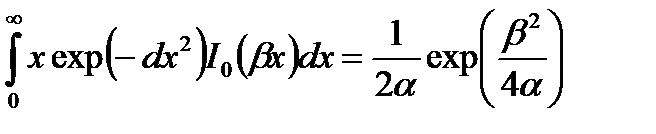получаем

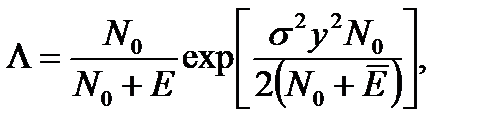
либо

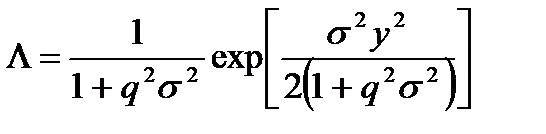, (8.18)

где

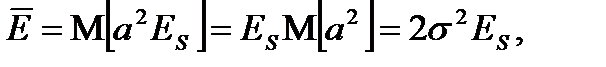(8.19)

- усредненная энергия сигнала.

Поскольку у ³ 0, отношение правдоподобия L является монотонной функцией у. Поэтому, как и в предыдущем случае алгоритм оптимального обнаружения определяется формулами (8.12) и (8.13). Таким образом, структурные схемы оптимального обнаружителя сигнала со случайными амплитудой и начальной фазой совпадают со схемами оптимального обнаружителя сигнала со случайной фазой (см.рис.8.2 и 8.3). Заметим, что операция извлечения квадратного корня в схеме на рис.8.2 не обязательна, так как алгоритм (8.12) эквивалентен сравнению у² c h². Применительно к схеме на рис.8.3 это означает, что безразлично, какова характеристика амплитудного детектора - линейная или квадратичная.

Так как алгоритм обнаружения по сравнению с предыдущим случаем не изменился, то и вероятность ложной тревоги определяется прежней формулой (8.14). Для расчета вероятности правильного обнаружения потребуется найти плотность вероятности достаточной статистики у при l = 1:

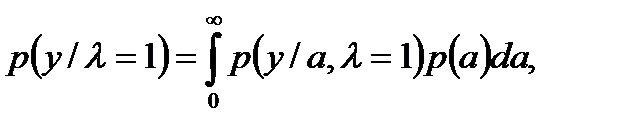
где р(а) определяется формулой (8.17), а

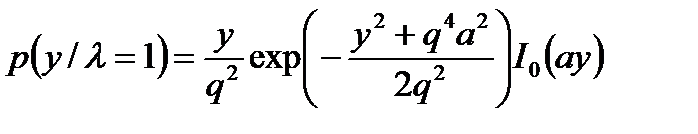
- плотность вероятности огибающей смеси сигнала и шума при фиксированном значении а. Вычисляя этот интеграл, получаем

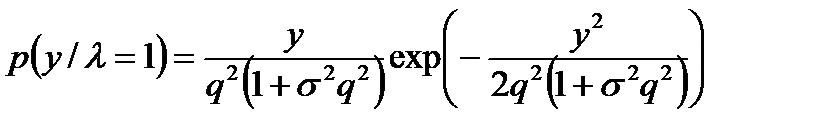
и затем находим вероятность правильного обнаружения

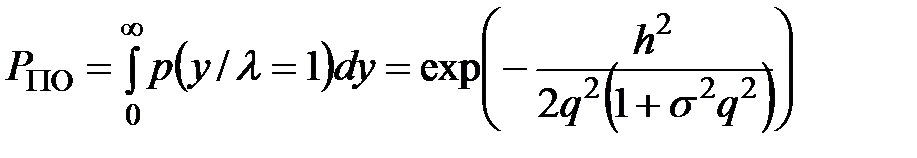. (8.20)

Эта формула вместе с (8.14) и определяет характеристики оптимального обнаружения сигнала со случайными амплитудой и начальной фазой. Сравнивать их с характеристиками обнаружения сигнала при известной амплитуде нужно при условии равенства энергий различных сигналов. Поэтому согласно (8.19) следует положить s² = 0,5. Учитывая это и исключая из (8.14) и (8.20) порог h, получаем

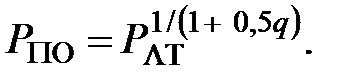(8.21)

Характеристики обнаружения, рассчитанные по формуле (8.21), показаны на рис.8.1 (штрих-пунктирные линии). Видно, что характеристики обнаружения в этом случае особенно сильно смещаются вправо в области больших значений вероятности правильного обнаружения (при Р_по ³ 0,9). Это связано с возможными замираниями при случайной амплитуде сигнала. Чтобы обеспечить достаточно большие вероятности правильного обнаружения при наличии таких замираний, необходимо значительное увеличение средней энергии сигнала. Наоборот, при малых вероятностей правильного обнаружения (Р_по < 0,3) флуктуации амплитуды облегчают обнаружение и характеристики сдвигаются влево.