Векторная диаграмма сигнала

Это изображение токов и напряжений на координатной плоскости через векторы, сопоставленные гармоническим колебаниям.

Векторы, представляющие на координатной плоскости гармонические колебания разных частот, будут вращаться против хода часов вокруг начала координат с разными угловыми скоростями. Их модули определяются амплитудами колебаний, а углы наклона в момент начала отсчета – значениями начальных фаз. Проекции векторов на ось абсцисс будут представлять собой косинусоидальные колебания, на ось ординат – синусоидальные. Они укажут, как будут изменяться во времени мгновенные значения токов и напряжений.

Пример:

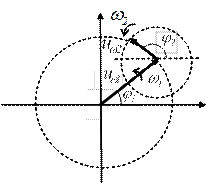
Рисунок 3.4 – Векторная диаграмма.

Достоинства: наглядность интерпретации спектрального разложения.

Недостатки: неудобство при представлении поведения во времени напряжения или тока.

СПЕКТРЫ СИГНАЛОВ

Виды спектров

Вид спектра зависит от характера сигнала.

Различают дискретные (линейчатые) и непрерывные (сплошные) спектры.

Спектр будет дискретным, если сигнал можно рассматривать как конечную сумму или ряд (бесконечную сумму) гармонических колебаний. Он представляется на спектральной диаграмме набором отдельных спектральных линий (линий, соответствующих амплитудам и фазам гармоник).

Дискретным спектром обладают периодические и квазипериодические (почти периодические) сигналы.

Периодическими называются сигналы, значения которых повторяются через определенные равные промежутки времени, называемые периодом. Особенность спектров периодических сигналов состоит в том, что частоты гармоник в них кратны основной частоте 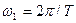. Такие спектры называют гармоническими.

Разновидностью непериодических сигналов являются квазипериодические. Это сигналы, значения которых приближенно повторяются через определенные промежутки времени, называемые почти периодом.

Пример: .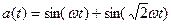

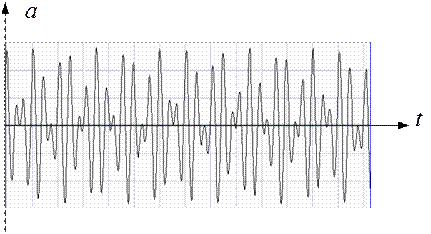
Рисунок 4.1 – Квазипериодический сигнал.

Особенность спектров квазипериодических сигналов состоит в том, что частоты гармоник в них не находятся в кратном отношении. Такие спектры не являются гармоническими.

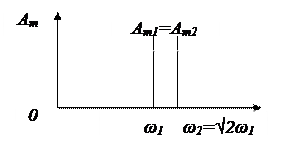
Рисунок 4.2 – Дискретный спектр.

Спектр будет непрерывным, если сигнал можно рассматривать как сумму бесконечно большого числа бесконечно малых по амплитуде гармонических колебаний, частоты которых располагаются бесконечно близко друг к другу. По оси ординат амплитудной спектральной диаграммы откладывается спектральная плотность амплитуд, фазовой – спектральная плотность фаз.

Непрерывным спектром обладают непериодические сигналы (одиночные импульсы, информационные сигналы), а также хаотические колебания (шумы).

Спектральная плотность амплитуд 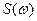- функция частоты, несущая информацию об амплитуде элементарных гармоник. Она характеризует интенсивность сплошного распределения амплитуд гармоник сигнала вдоль оси частот. Спектральная плотность амплитуд сигнала на любой частоте ω равна суммарной амплитуде спектральных составляющих, попадающих в малую полосу Δω в окрестности частоты ω, пересчитанной к полосе 1 Гц:

.

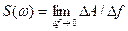Имеет размерность В/Гц или А/Гц.

Рисунок 4.3 – Амплитудная спектральная диаграмма ОПИ.

Спектральная плотность фаз 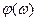– функция частоты, несущая информацию о фазе элементарных гармоник.

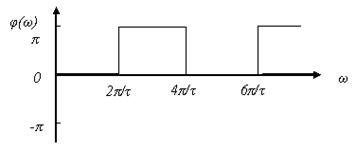
Рисунок 4.4 – Фазовая спектральная диаграмма ОПИ.

Различают ограниченные и неограниченные спектры.

Ограниченным называют спектр, имеющий конечный интервал частот, в котором расположены все спектральные линии периодического либо квазипериодического сигнала или на котором отлична от нуля спектральная плотность непериодического сигнала. Если этот интервал бесконечен, то спектр является неограниченным

Рисунок 4.5 – Ограниченный спектр.