Аппаратурно можно получить текущий спектр сигнала

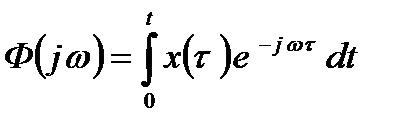. (2.26)

При большом времени анализа текущий спектр может быть достаточно хорошим приближением к истинному спектру. При построении анализаторов спектра можно использовать выражение (2.26) в чистом виде, т.е. произвести все мате­матические операции над сигналом согласно выражению (2.26). Этот тип анализаторов используется достаточно широко в связи с развитием цифровой вычислительной техники. Однако наиболее распространены анализаторы спектра с ис­пользованием резонаторов.

Простейшим резонатором является колебательный контур, изображенный на рис. 2.18.

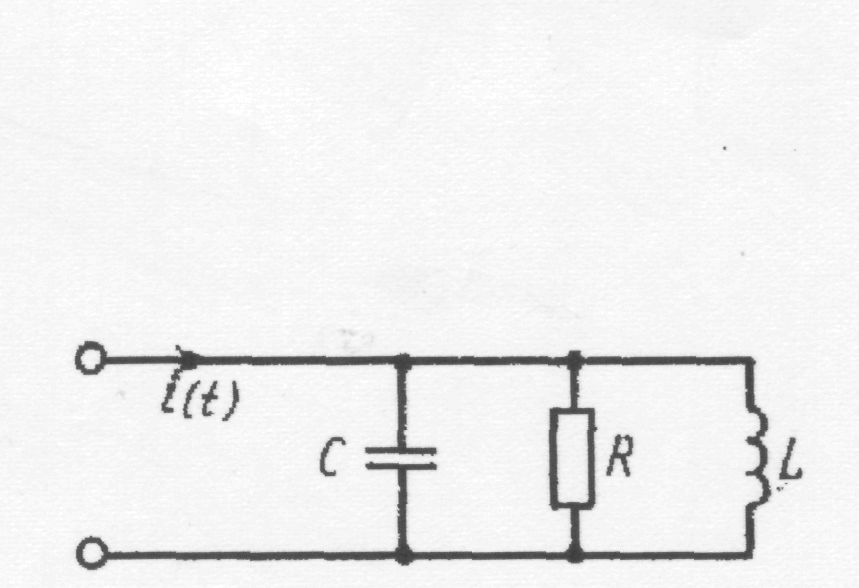
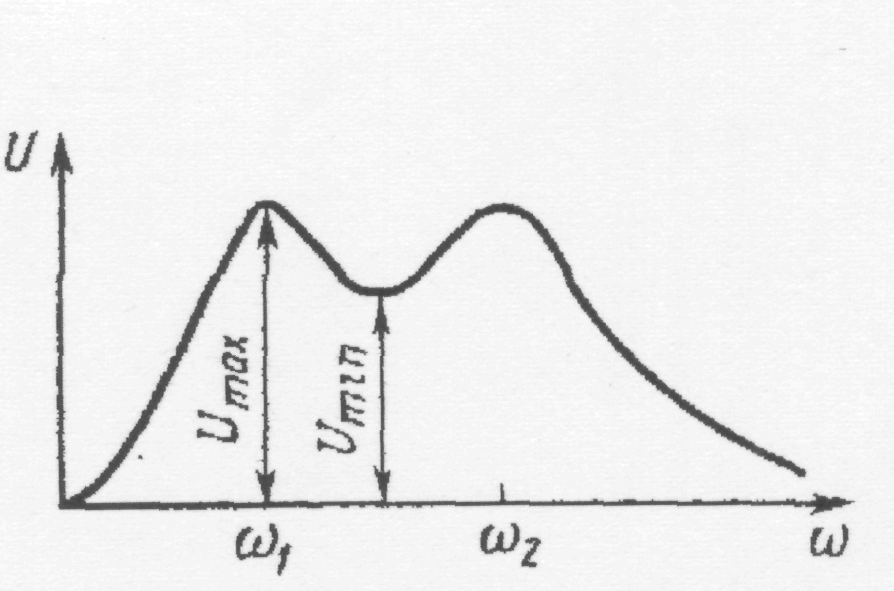
Рис. 2.18. Схема резонатора Рис. 2.19. К вопросу о разрешающей

возможности анализатора

Характеристики анализаторов спектра.

Минимальный интервал по частоте между двумя гармоническими сигналами, при котором они разделяются анализатором, называют разрешающей способностью анализатора спектра. Пусть на колебательный контур (Рис. 2.18) подана сумма двух гармонических сигналов

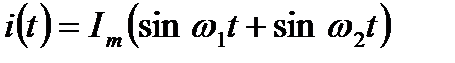. (2.27)

Если изменять собственную частоту контура от 0 до ∞ и фик­сировать максимальное значение напряжения на контуре, то можно получить зависимость, представленную на рис. 2.20.

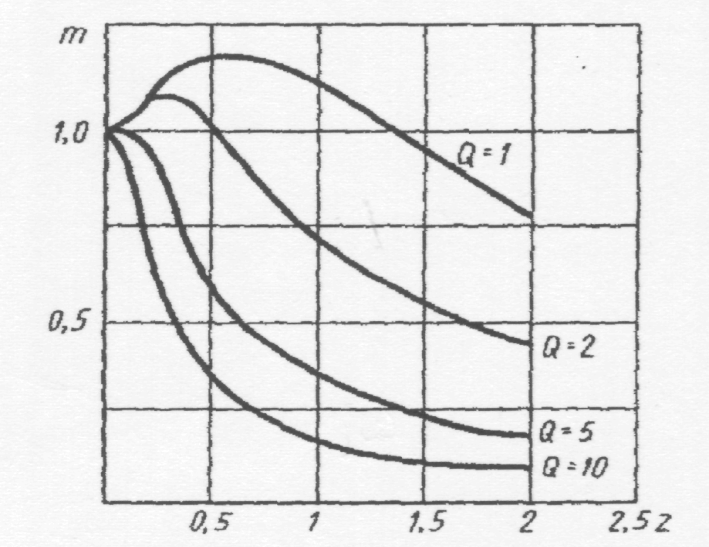
Рис. 2.20. Зависимость разрешающей способности от добротности резонатора

Разрешающей способностью будет такая разность частот ω2 – ω1, при которой U_min /U_max = m (m принимают равным 0,5 или ).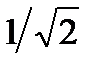

Разрешающая способность резонатора зависит от вида его частотной характеристики. Например, для рассматриваемого контура выражение для t можно получить в виде

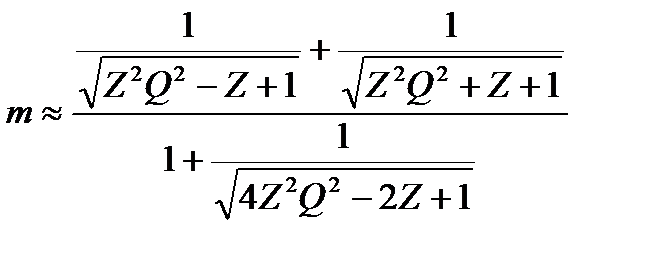, (2.28)

где Z = 2(ω₂ – ω₁)/( ω₂ + ω₁).

Вид зависимости m от Z при разных значениях добротности приведен на рис. 2.20. Если измерять напряжение на контуре вольтметром среднеквадратических значении, то получим следующее уравнение для определения разрешающей способности:

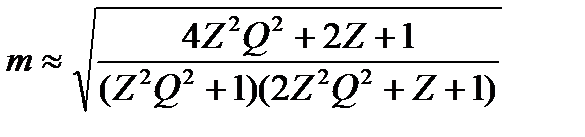. (2.29)

Для разрешающей способности найти выражение при па­раллельном анализе сложнее, чем при последовательном. По­кажем качественно, как можно определить разрешающую спо­собность параллельного анализатора. Пусть на анализатор из семи фильтров воздействует сумма двух равных по амплитуде гармоник с частотами ω_l и ω₂.

Резонансные кривые фильтров приведены на рис. 2.21,а. Если соединить плавной кривой отклики различных фильтров на возбуждающее воздействие, то получим двугорбую кривую (Рис.2.21,6), но которой устанавливают разрешающую способность анализаторов последовательного действия.

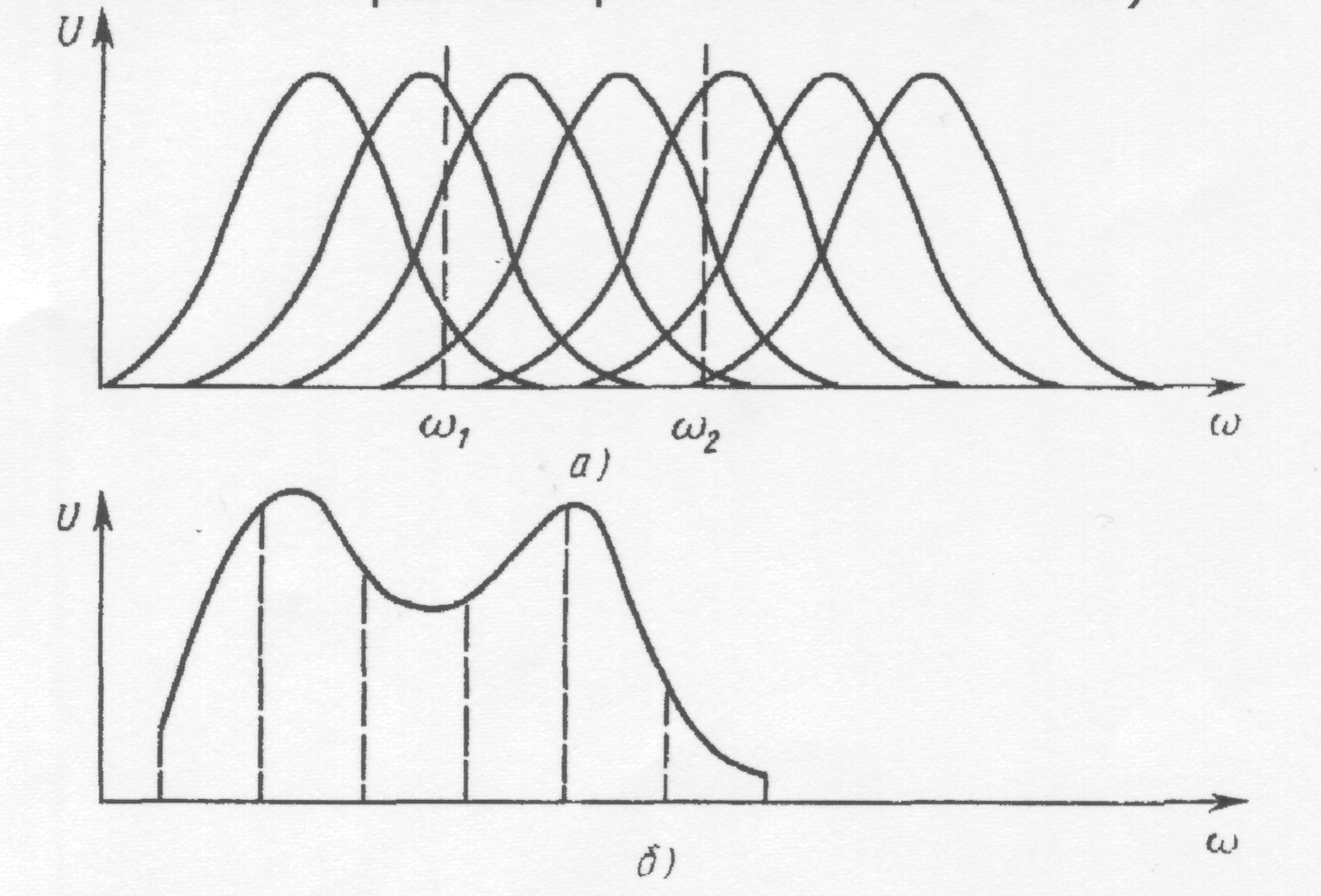
Рис. 2.21. Резонансные кривые фильтров

Важной характеристикой анализаторов спектра является и время (скорость) анализа, которое характеризует, насколько быстро можно провести анализ сигнала в определенном диапазоне частот. Время параллельного анализа зависит от времени установления колебаний и резонаторах, (время съема показаний с резонаторов обычно невелико).

Следующей характеристикой анализаторов спектра является полоса анализируемых частот. Она указывает частотный диапазон сигналов, которые могут исследоваться данным анализатором спектра. Для увеличения полосы анализируемых частот анализаторы спектра выполняют многодиапазонными. В анализаторах спектра обычно имеется возможность иссле­довать сигналы не во всем диапазоне, а в части его, называемой полосой обзора, что позволяет повысить точность анализа сигналов.

Как и все электронные приборы, анализаторы спектра явля­ются измерительными устройствами и характеризуются такими погрешностями, как погрешность по амплитуде и погрешность по частоте. Погрешность по частоте показывает, с какой точностью может быть определен интервал частот между со­ставляющими спектра или действительное значение частоты этих составляющих.

Погрешность по амплитуде определяется инструментальными погрешностями анализатора и зависит от спектра исследуемого сигнала. Реальный резонатор имеет отличную от нуля во всем диапазоне частот амплитудно-частотную характеристику. Вследствие этого напряжение на нем определяется всеми составляющими спектра сигнала, а не только составляющей с частотой, равной собственной частоте резонатора. Это приводит к погрешности, но амплитуде. Погрешности анализаторов спектра связаны также со временем анализа.

Динамическая разрешающая способность. Рассмотрим последовательный анализ спектра. При этом вместо изменения собственной частоты резонатора линейно изменим частоту поданного воздействия. Результаты анализа применимы и для случая с изменением собственной частоты резонатора. При линейном изменении частоты воздействия амплитудно-частотная характеристика резонатора деформируется, но срав­нению со статической характеристикой, которая снимается при установившихся значениях частот. Деформация резонансной кривой (Рис. 2.22) может характеризоваться рядом параметров: относительным изменением значения максимума

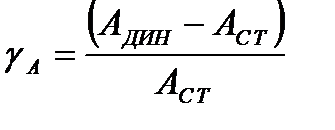, (2.30)

относительным смещением максимума динамической ха­рактеристики относительно максимума статической характе­ристики

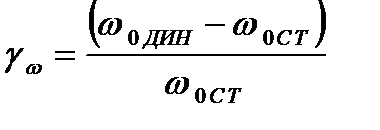, (2.31)

относительный расширением полосы пропускания

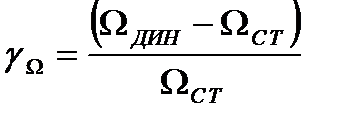. (2.32)

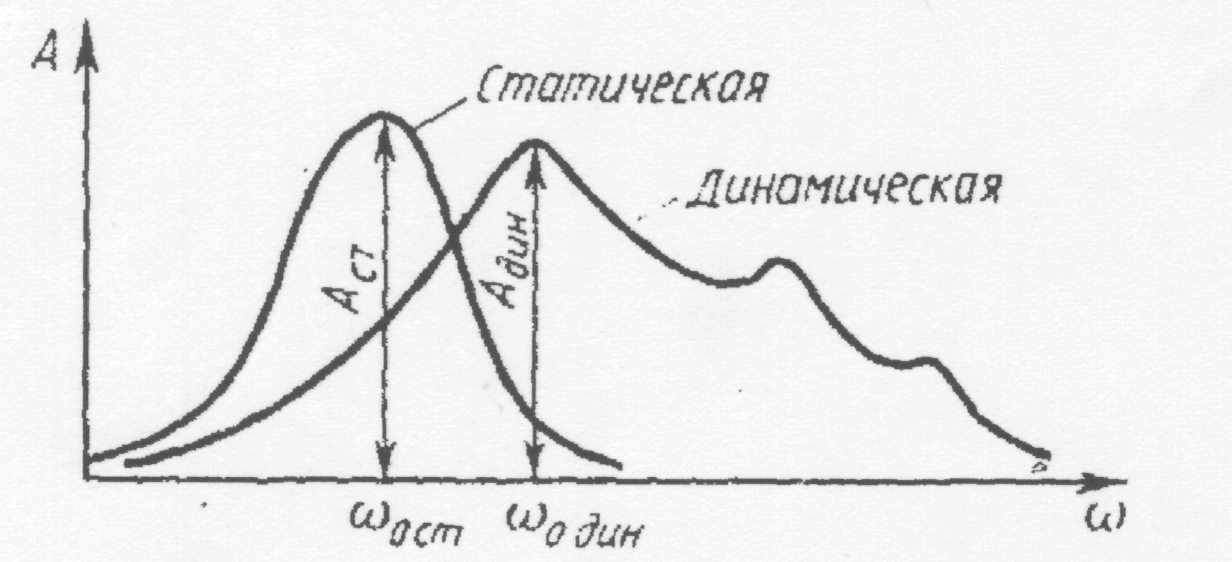
Рис. 2.22. Динамическая характеристика резонатора

Чтобы получить выражения для указанных параметров вос­пользуемся выводом, сделанным ранее. В таблице 2.1 приведены выражения этих параметров для трех типов колебательных систем: одиночного контура, n слабо связанных контуров, двух связанных контуров при критической связи. Пусть с помощью характериографа анализируется сквозной тракт радиоприемника с полосой пропускания 10кГц на частоте 7МГц (41 м). Выберем скорость изменения частоты характериографа 100МГц/с. Для данного случая μ=0,64. Допустим, что избирательная система радиоприемника состоит из четырех слабо связанных контуров. По формулам таблицы 2.1 находим:

Y_а = –5%,Y_ω = 0,08%, Y_W = 10%.

Таблица 2.1

Погрешности	Тип колебательной системы
Одиночный контур	Слабо связанных контуров	Два критически связанных контура
γА	– μ2 / 2	–1,12μ2	1,25μ2
γω	– μΩ / ω0		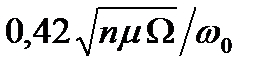– 0,45μ1×3 Ω / ω0
γΩ	1,25μ2	1,24μ2	12,5μ2

Полученные данные показывают, что при выбранной скорости анализа погрешности Y_a и Y_ω несущественны для установок качественных показателей радиоприемники, а расширение полосы пропускания необходимо принимать во внимание.

Примечание. Ω – полоса пропускания колебательной системы, μ = 4λ/Ω – обобщенный параметр, λ – скорость изменения частоты.

Время анализа. Как известно, время установления колебаний в резонаторе зависит от вида амплитудно-частотной характеристики резонатора и его полосы пропускания. Чем уже полоса пропускания фильтра, тем больше время установления колебаний в нем. Для любого линейного четырехполюсника справедливо соотношение

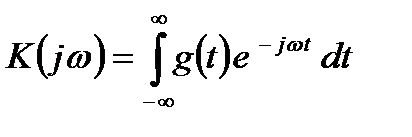, (2.33)

т.е. комплексный коэффициент передачи К(jω) есть ни что иное, как спектр функции g(t), представляющей собой реакцию четырехполюсника па входное воздействие в виде дельта-функции. Необходимо установить связь между шириной частотной характеристики и длительностью отклика. В теории сигналов под шириной спектра сигналов обычно понимают полосу частот, в которой сосредоточена основная доля (90%) энергии сигнала, т.е.

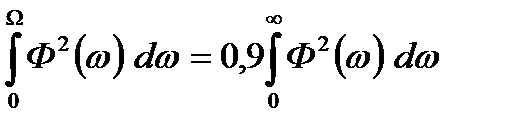. (2.34)

Для определения длительности сигналов применяют тот же критерий. Под длительностью сигнала понимают часть импульса, в которой сосредоточена подавляющая часть (90%) энергии импульса, т. е.

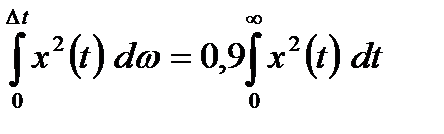. (2.35)

Можно написать независимо от определений ширины полосы (Ω) и времени установления резонаторов t_У, что

. (2.36)

Значение С зависит от типа резонатора и определений 0 и t_У. Наименьшее значение коэффициента С будет для резонатора с колоколообразной амплитудно-частотной характеристикой. К такой характеристике приближается характеристика многока­скадного слабо связанного резонансного усилителя.

Время анализа для анализаторов:

Параллельного

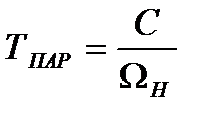, (2.37)

где Ω_ННН – полоса пропускания самого низкочастотного фильтра анализатора;

последовательного

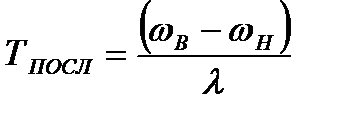, (2.38)

где ω_В, ω_Н – диапазон анализируемых анализатором частот.

Сравним время анализа этих анализаторов. Примем, что разрешающая способность анализаторов – постоянная во всем диапазоне. Это означает, что параллельный анализатор имеет набор одинаковых по полосе пропускания фильтров. Пусть

Тогда время анализа последовательного анализатора

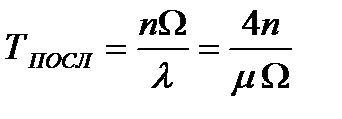, (2.39)

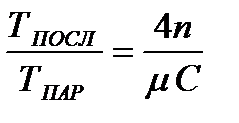, (2.40)

обычно для анализаторов выполняется условие

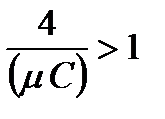. (2.41)

Следовательно, время последовательного более чем в n раз превосходит время параллельного анализа. Однако следует помнить, что высокая скорость анализа параллельных анализаторов достигается их структурной избыточностью (n резонаторов).