Векторная диаграмма
Векторную диаграмму рассмотрим на примере изменяющейся по синусоидальному закону ЭДС: 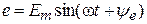 .
.
Рассмотрим прямоугольную систему координатных осейNOMи условимся откладывать положительные углы против вращения часовой стрелки.
Расположим вектор ОА под углом 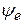 к оси ON. Пусть длина этого вектора равна амплитуде ЭДС к оси ON. Пусть длина этого вектора равна амплитуде ЭДС 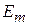 . Будем вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. По истечении промежутка времени t вектор ОА повернется на угол . Будем вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. По истечении промежутка времени t вектор ОА повернется на угол 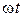 и составит с осью ON угол и составит с осью ON угол 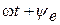 . Тогда величина его проекции на ось OM в принятом масштабе даст значение ЭДС для момента времени t: . Тогда величина его проекции на ось OM в принятом масштабе даст значение ЭДС для момента времени t: 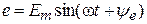 . .
| 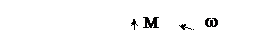
|
Полный цикл изменений ЭДС получится за один полный оборот вектора ОА.
Таким образом, синусоидальную (косинусоидальную) функцию можно охарактеризовать вектором, длина которого определена ее амплитудным значением, а направление – ее начальной фазой. При этом, положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов. В результате получаем векторную диаграмму.
Векторные диаграммы удобны при сложении или вычитании синусоид одинаковой частоты. При сложении нескольких синусоид необходимо складывать их мгновенные значения, т. е. проекции векторов, изображающих эти синусоиды. В результате такого сложения геометрическую сумму векторов определит результирующий вектор, который будет характеризовать результирующую синусоиду.
Дата добавления: 2015-12-11; просмотров: 890;
