Установившийся режим в цепи с параллельным соединением активного сопротивления, индуктивности и емкости

| При параллельном соединении сопротивления R, индуктивности L и емкости С мгновенное значение тока i всей цепи, согласно первому закону Кирхгофа, равно: 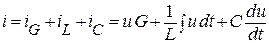 . .
|
Положим  . Тогда
. Тогда 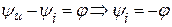 .
.
Откуда 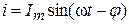 .
.
Подставляя эти выражения в записанное уравнение, получим:
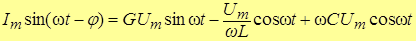 .
.
Это уравнение справедливо для любого момента времени, поэтому, как и в случае последовательного соединения элементов, рассмотрим два момента 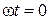 и
и  .
.
Задавая 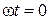 , получим:
, получим: 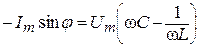 или
или  .
.
Задавая  , получим:
, получим: 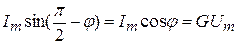 .
.
Далее действуем по аналогии с предыдущим случаем. Возводя в квадрат каждое из этих выражений, и, суммируя, получаем:
 ,
,
где  – полная проводимость цепи.
– полная проводимость цепи.
При этом, 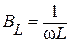 – индуктивная,
– индуктивная,  – емкостная,
– емкостная, 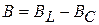 – реактивная проводимости цепи.
– реактивная проводимости цепи.
Угол сдвига фаз 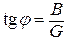 , откуда
, откуда  .
.
Построим векторную диаграмму действующих значений токов для φ > 0:

| Задаемся положением вектора приложенного напряжения U. Активный ток  совпадает по фазе с напряжением U,индуктивный ток совпадает по фазе с напряжением U,индуктивный ток 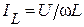 отстает от напряжения на отстает от напряжения на 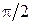 , емкостный ток , емкостный ток 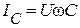 опережает напряжение на опережает напряжение на 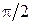 , реактивный ток , реактивный ток 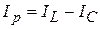 . Тогда действующее значение тока всей цепи . Тогда действующее значение тока всей цепи
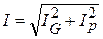 . .
|
Полученный треугольник носит название треугольника токов. Если все стороны треугольника поделить на величину напряжения U, то получим подобный треугольник, который носит название треугольника проводимости.

|
Анализируя треугольники сопротивлений и проводимостей, легко обнаружить связь между соответствующими параметрами:
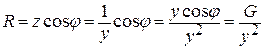 , аналогично
, аналогично 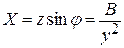 .
.
Проводя подобные преобразования для проводимостей, получим:
 ;
; 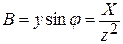 ;
; 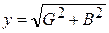 .
.
Дата добавления: 2015-12-11; просмотров: 948;
