При различении детерминированных сигналов

Достаточная статистика y, определяемая при различении детерминированных сигналов, согласно выражению (9.9) зависит от реализации x(t), которая из-за действия шума меняется. В общем случае y следует рассматривать как случайную величину, которая получится, если на место реализации x(t) подставить случайный процесс x(t):

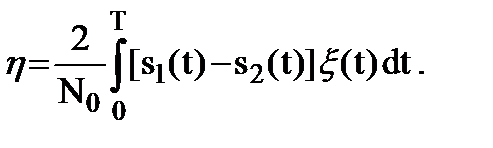(9.11)

При гауссовском белом шуме n(t) процесс x(t) является гауссовским случайным процессом и случайная величина h, определяемая линейным оператором преобразования, каковым является интегрирование, также имеет гауссовское распределение. И так как величина l неизвестна, случайная статистика h определяется двумя условными плотностями вероятности: p_sn1(y) при l = 1и p_sn2(y) при l = 0.

Найдем числовые характеристики этих распределений при условии, что энергии сигналов s₁(t) и s₂(t) равны, и следовательно q₁² = q₂² = q².

1. Пусть l = 1. Тогда 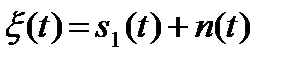. При этом

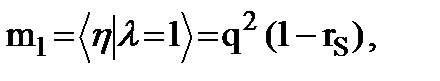(9.12)

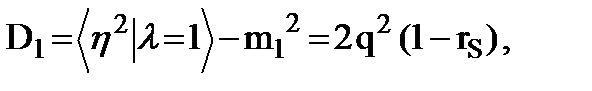(9.13)

где коэффициент взаимной корреляции между сигналами s₁(t) и s₂(t):

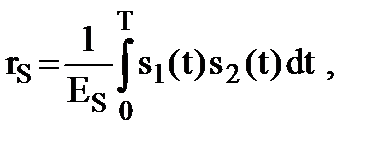(9.14)

2. Пусть l = 0. Тогда x(t) = s₂(t) + n(t). При этом

m₂=<h/l=0>= – q²(1-r_s) , (9.15)

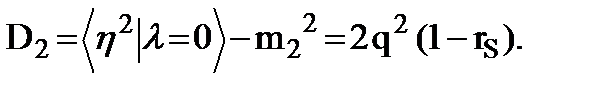(9.16)

Таким образом, числовые характеристики зависят не только от отношения сигнал/шум, но и от коэффициента взаимной корреляции между сигналами s₁(t) и s₂(t).

Графики условных плотностей вероятности достаточной статистики p_sn1(y) и p_sn2(y)

Рис.9.5

Располагая p_sn1(y) и p_sn2(y), можно найти вероятность полной ошибки Р_ош. Методика здесь используется та же, что и при определении Р_ош при обнаружении сигнала (7.3). Отличие состоит в том, что использование таких терминов как пропуск сигнала и ложная тревога, теряет смысл, так как сигнал s₁(t) всегда присутствует на входе различителя.

Согласно (7.3) выражение для Р_ош запишем в следующей форме:

Р_ош = Р(Н₁)Р(s₂/s₁) + Р(Н₂)Р(s₁/s₂) , (9.17)

где Р(Н₁), Р(Н₂) - априорные вероятности наличия соответственно сигналов s₁(t) и s₂(t) на входе различителя; P(s₂/s₁) - вероятность принятия решения о том, что на входе сигнал s₂(t), когда в действительности существует s₁(t); P(s₁/s₂) - вероятность принятия решения о том, что на входе сигнал s₁(t), когда в действительности существует s₂(t). Если Р(Н₁) = Р(Н₂) = 0,5, то выражение (9.17) примет вид

Р_ош= 0,5[Р(s₂/s₁) + P(s₁/s₂)]. (9.18)

Если к тому же равны и энергии сигналов s₁(t), s₂(t), то порог h = 0 и, в силу симметричности кривых p_sn1(y), p_sn2(y) относительно начала координат (рис.9.5), условные вероятности P(s₂/s₁), P(s₁/s₂), определяемые формулами

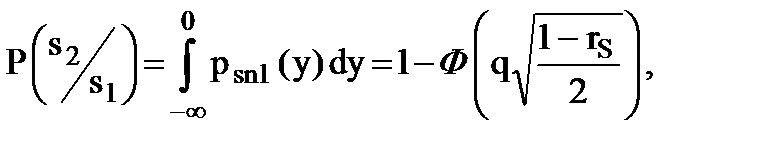(9.19)

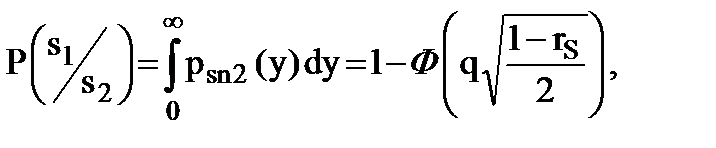(9.20)

равны между собой

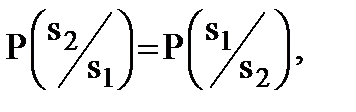(9.21)

Тогда

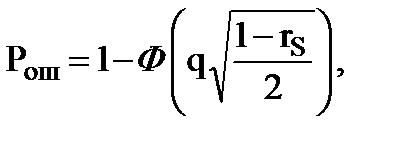(9.22)

Вероятность полной ошибки Р_ош, таким образом, определяется условной вероятностью принятия решения при различении одного из сигналов, если их энергии равны.