При различных видах манипуляции
В теории дискретной радиосвязи для характеристики потенциальной помехоустойчивости различителя, оптимального по критерию идеального наблюдателя, используется зависимость вероятности полной ошибки Рош от отношения сигнал/шум q:
Рош = f(q). (9.23)
При различении детерминированные сигналы s1(t) и s2(t) могут отличаться амплитудой, частотой или начальной фазой, представляя собой амплитудно-манипулированные (АМн), частотно-манипулированные (ЧМн) или фазо-манипулированные (ФМн) колебания. Представляет интерес найти зависимости (9.23) различителей АМн, ЧМн и ФМн сигналов и сравнить эти зависимости между собой.
| t |
| t |
| t |
| АМн |
| ЧМн |
| ФМн |
| t |



| 0 1 0 1 1 1 0 |
| в) |
| б) |
| а) |
| s(t,l) |
В различителе АМн сигналов будем полагать, что s2(t) = 0. В этом случае символ “1” связан с передачей сигнала s1(t), а символ “0” - с паузой (рис.9.6,а). Работа такого различителя фактически сводится к оптимальному обнаружению сигнала s1(t) по критерию идеального наблюдателя
Рош = Р(Н1)Рпроп + Р(Н0)Рлт , (9.24)
в котором для вычисления (9.23) можно считать, что присутствие и отсутствие сигнала априорно равновероятно. Принимая Р(Н1) = Р(Н0) = 0,5. В этом случае величина порога h, необходимого для работы обнаружителя, будет определяться только отношением сигнал/шум:
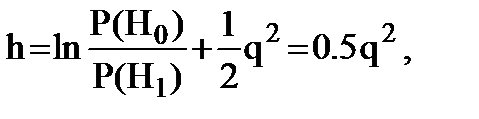 (9.25)
(9.25)
В свою очередь, вероятности Рпроп и Рлт при использовании порога (9.25) будут равны между собой (рис.9.7,а). Действительно, согласно (8.4) и (8.5) имеем
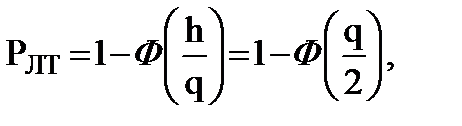 (9.26)
(9.26)
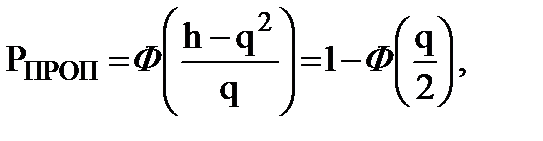 (9.27)
(9.27)
так как Ф(-z) = 1 – Ф(z).
Подставив (9.26) и (9.27) в формулу (9.24), получаем зависимость вероятности полной ошибки от отношения сигнал/шум при различении Амн сигналов
Рош Амн = 1 – Ф(q/2). (9.28)
Вероятности ошибок ЧМн и ФМн различителей могут быть найдены на основании материала параграфа 3 данной лекции. Требуется только найти коэффициенты взаимной корреляции rs , которые будут различны для ЧМн и ФМн сигналов.
В различителе ЧМн сигналов символ “1” связан с сигналом s1(t) = a0×cos w1t , а символ “0” – с сигналом s2(t) = a0×cos w2t , которые имеют одинаковую длительность Т, но отличаются между собой частотами w1 и w2 (рис.9.6,б). Если длительность символов Т достаточно велика, то 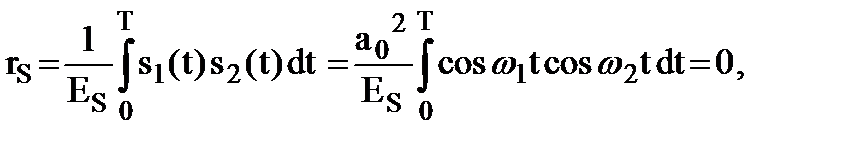
Тогда согласно (9.22)
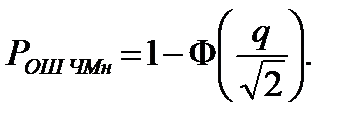 (9.29)
(9.29)
При этом m1 = q2, m2 = - q2, D1 = D2 = 2q2 (рис.9.7,б).
В различителе ФМн сигналов будем связывать символ “1” с сигналом s1(t) = a0cosw0t, а символ “0” - с сигналом s2(t) = a0cos(w0t + p) = - a0cosw0t, которые имеют одинаковую длительность Т, но отличаются между собой начальной фазой на величину p (рис.9.6,в). Это приводит к тому, что сигнал s1(t) противоположен по знаку к сигналу s2(t) и, значит
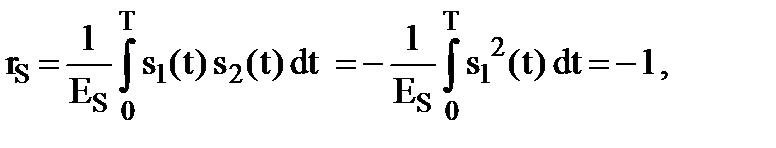
Тогда согласно (9.22)
Рош фмн = 1 - Ф(q) . (9.30)
При этом m1 = 2q2, m2 = -2q2, D1 = D2 = 4q2 .

Графики (9.28) - (9.30) для сравнения между собой представлены на рис. 9.8 в линейном (а) и логарифмическом масштабе (б). Вторая форма представления графика обычно используется в расчетах. Из рис.9.8 следует, что у различителя ФМн сигналов кривая Рош фмн = f(q) идет левее и ниже остальных. Это означает, что помехоустойчивость ФМн различителя наибольшая.
| 10-2 |
| q |
| 10-1 |
| 0.5 |
| АМ |
| ЧМ |
| ФМ |
| q |
| 0.5 |
| Рош |
| а) |
| б) |
Дата добавления: 2016-01-26; просмотров: 1145;
