Оценка энергетических и неэнергетических параметров сигнала

Пусть на входе измерителя действует случайный процесс, представляющий собой сумму детерминированного сигнала s(t,l) с неизвестным параметром l и гауссовского белого шума n(t) со спектральной плотностью N₀:

x(t) = s(t,l) + n(t) . (10.6)

Оптимальный измеритель определяет математическую операцию, которую необходимо выполнить над реализацией x(t) случайного процесса на интервале времени [0,T], чтобы найти оптимальную оценку параметра l по выбранному критерию оптимальности. При этом считается, что задача обнаружения сигнала решена и на входе измерителя действительно существует сумма (10.6).

На практике для оценки параметров сигналов наиболее часто применяют два метода:

- метод максимума апостериорной плотности вероятности;

p[l / x(t)] = k₁ p(l) L(l), (10.7)

здесь k₁ - коэффициент пропорциональности; р(l) - априорная плотность вероятности параметра l, L(l) - функция правдоподобия.

- метод максимума функции правдоподобия.

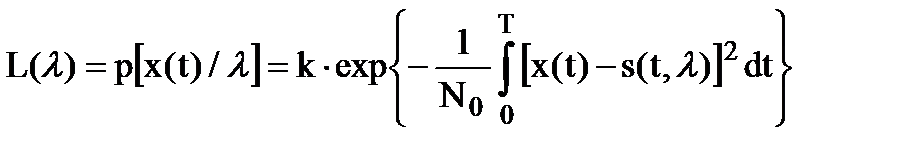. (10.8)

Второй метод используется в тех случаях, когда априорная плотность вероятности р(l) неизвестна для оцениваемого параметра l. Оценки, найденные по этому методу, называются правдоподобными оценками. Правдоподобная оценка и оценка, найденная по методу максимума апостериорной плотности вероятности, совпадают между собой, если параметр l имеет равномерное распределение.

Если функция правдоподобия имеет один максимум, то правдоподобная оценка l находится из решения уравнения

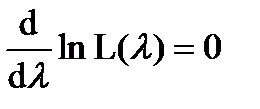, (10.9)

или

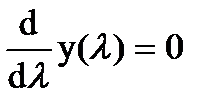, (10.10)

где y(l) является достаточной статистикой, определяемой по формуле (10.11)

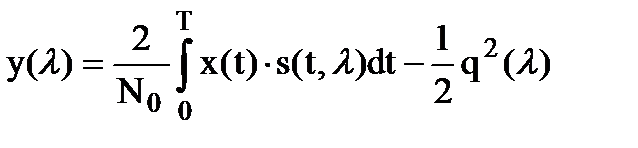, (10.11)

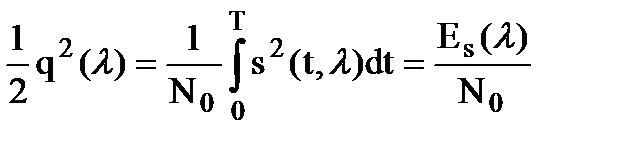. (10.12)

Достаточная статистика вычисляется как разность между корреляционным интегралом и половиной квадрата отношения сигнал/шум. При этом, как корреляционный интеграл, так и отношения сигнал/шум в общем случае зависят от параметра l.

Все оцениваемые параметры можно разделить на энергетические и неэнергетические. Энергетическим называется такой параметр, от которого зависит энергия сигнала и, соответственно, отношение сигнал/шум. К энергетическим параметрам относятся амплитуда и длительность сигнала. Неэнергетическим называется такой параметр, от которого энергия сигнала и отношение сигнал/шум не зависят. К неэнергетическим параметрам относятся начальная фаза, частота и т.д.

Для неэнергетического параметра в качестве достаточной статистики у(l) вместо выражения (10.11) удобнее использовать соотношение

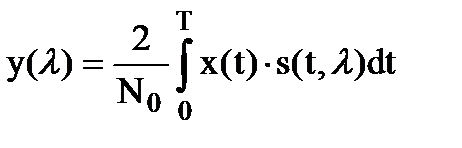. (10.13)

Таким образом, измеритель, оптимальный по критерию максимума функции правдоподобия, должен сформировать достаточную статистику (10.11) или (10.13), а затем для нахождения оценки параметра решить уравнение (10.8).