Сигнальная и шумовая функции. Дисперсия правдоподобной оценки параметра сигнала

Из-за действия шума статистика у(l) , будет случайной величиной. Случайная статистика может быть получена, например, в случае оценивания неэнергетического параметра. Для этого необходимо подставить в формулу (10.8) вместо реализации x(t) случайный процесс x(t) :

x(t) = s(t, l₀) + n(t) , (10.18)

где l₀ - истинное значение параметра.

В результате имеем

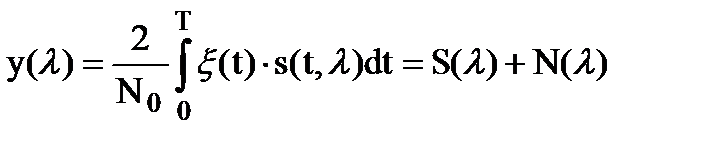, (10.19)

где

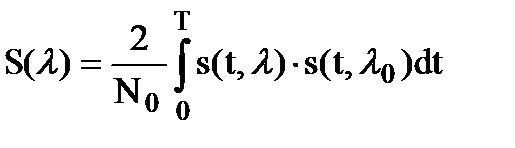, (10.20)

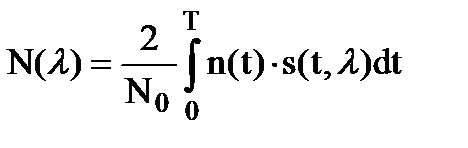. (10.21)

Зависимость S(l) называется сигнальной функцией , а зависимость N(l) - шумовой функцией .

Сигнальная функция S(l) представляет собой корреляционный интеграл между сигналом с истинным значением параметра l₀ и этим же сигналом, но с оцениваемым параметром l, играющим роль аргумента. Интеграл берется за время существования сигнала. Пример графика S(l) показан на след. рисунке

Максимум S(l) достигается при l = l₀, соответствуя квадрату отношения сигнал/шум:

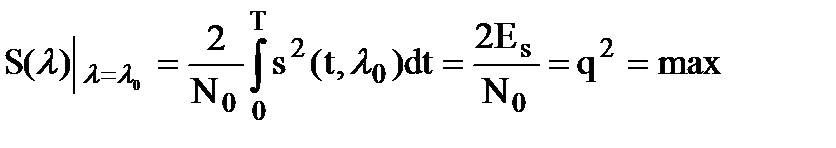. (10.22)

Так как максимум S(l) достигается при l = l₀, то

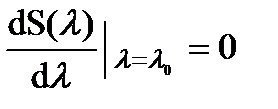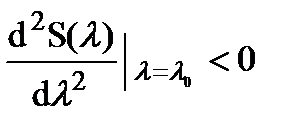. . (10.23)

Функция S(l) симметрична относительно вертикальной прямой, проходящей через точку l = l₀, так что

S(l - l₀) = S(l₀ - l) . (10.24)

Шумовая функция N(l) представляет собой корреляционный интеграл между шумом n(t) и сигналом s(t,l) с оцениваемым параметром, играющим роль аргумента. Для гауссовского стационарного шума n(t) шумовая функция является стационарным гауссовским случайным процессом параметра l с нулевым математическим ожиданием

< N(l) > = 0 , (10.25)

и корреляционной функцией, определяемой сигнальной функцией:

R_N(l₂ - l₁) = < N(l₁)N(l₂) > = S(l₂-l₁). (10.26)

С помощью сигнальной функции можно оценить разрешающую способность измерителя. Действительно, если на входе действуют два сигнала s(t,l₀₁),s(t,l₀₂), отличающиеся между собой истинными значениями параметров l₀₁,l₀₂ , то на выходе измерителя появятся два сигнала s₁(l), s₂(l) в области l.

Два сигнала s(t,l₀₁), s(t,l₀₂) могут быть надежно выделены и их параметры раздельно измерены; если разность |l₀₂ - l₀₁| превышает разрешающую способность измерителя dl :

|l₀₂ - l₀₁| ³ dl . (10.27)

Разрешающая способность dl согласно критерию Релея определяется как разность (l₀₂ - l₀₁) , которая соответствует ширине сигнальной функции (рис.). Уровень, на котором определяется S(l), может быть различным. На рис. уровень для определения dl выбран нулевым.

Сигнальная функция S(l) используется также для нахождения степени разброса оценки вокруг l₀ , если 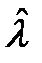является несмещенной оценкой .

При выполнении этого условия степень разброса оценки вокруг l₀ будет определяться дисперсией оценки:

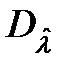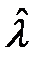= < ( -l₀)² > . (10.28)

На практике, вместо дисперсии, для характеристики степени разброса 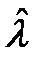вокруг l₀ используется среднее квадратическое отклонение (СКО), равное корню из дисперсии, так как размерности оценки и СКО совпадают. Можно показать, что дисперсия правдоподобной оценки параметра сигнала обратно пропорциональна взятой с обратным знаком кривизне сигнальной функции в точке истинного значения параметра

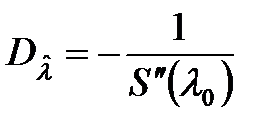, (10.29)

где 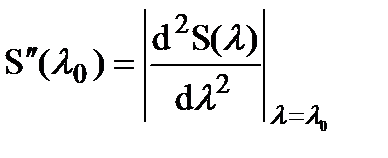- кривизна S(l).

Формула (10.29) имеет важное значение. С ее помощью можно определять потенциальную точность оптимального измерителя, располагая только отношением сигнал/шум q, формой сигнала s(t,l) и выбором оцениваемого параметра l, не прибегая к анализу работы конкретного измерителя.

Й семестр