Собственная информация

Рассмотрим дискретную случайную величину x с известным зако­ном распределения, заданным рядом вероятностей, в котором каждому возможному значению случайной величины х₁, х₂, ..., х_m сопоставлена соответствующая вероятность p₁, p₂,…,p_m

Известно, что для характеристики тех или иных черт распреде­ления случайной величины используются числовые характеристики, определённые как математические ожидания или усреднённые значения некоторых функций случайной величины. Если в качестве ус­редняемой функции выбрать логарифм вероятности возможного значе­ния, то получим новую числовую характеристику случайной величины:

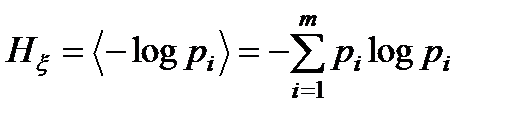(1.4)

Эта числовая характеристика называется энтропией случайной величины x. Энтропия характеризует в среднем неопреде­лённость случайной величины до испытания. Само слово происходит от греческих слов "en" и "trope", что означает "поворот", "прев­ращение", " обращение".

В дискретной радиосвязи сообщение состоит из набора символов. Совокупность всех возможных символов образует алфавит. Примерами дискретных сообщений являются, например, слова русского текста, алфавит которого состоит из 32 букв. Каждое слово есть сообщение, состоящее из букв, являющихся в данном случае символами.

Если проанализировать тексты на русском языке, то можно заме­тить, что одни буквы появляются чаще, а другие реже. Используя статистическое определение вероятности, можно определить вероят­ность появления той или иной буквы. Например, в русском литера­турном тексте вероятности появления таких букв, как О, Е, А, со­ответственно равны: р_о = 0,11; р_e= 0,089; р_a=0,076. Это наиболее часто появляющиеся буквы. Редкими буквами являются Щ, Э, Ф. Их вероятности появления соответственно равны р_щ= 0,003; p_э= 0,002; р_ф= 0,002. Буква О появляется чаще, чем буква Ф, в 50 раз.

Рассмотрим дискретное сообщение в общем виде. Пусть алфавит состоит из m символов. Все символы алфавита х₁, x₂, ..., х_m, если их пронумеровать хотя бы мысленно, можно рассматривать как возможные значения дискретной случайной величины x, с извест­ным рядом вероятностей.

Если считать, что появление 1-го символа, скажем х_i, пол­ностью устраняет имеющуюся ранее неопределенность, то с появлением этого символа получатель получает следующее коли­чество информации:

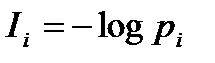, (1.5)

где р_i -априорная вероятность появления символа х_i.

Поставим теперь вопрос: какое количество информации I получит в среднем получатель при появлении любого одного символа из алфа­вита m ? Для ответа на этот вопрос необходимо (1.5) усреднить по всем символам алфавита :

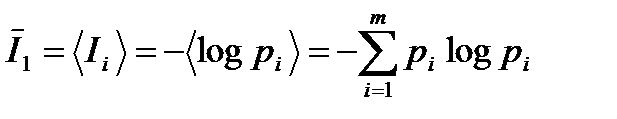. (1.6)

Заметим, что формулы (1.4) и (1.6) полностью совпадают. Это означает, что энтропия определяет среднее количество информации, приходящейся на один символ алфавита дискретного сообщения:

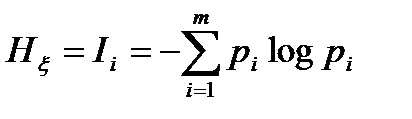. (1.7)

Наибольшая неопределённость дискретной случайной величины имеет место тогда, когда все её возможные значения равновероятны:

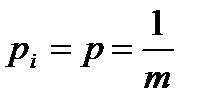. (1.8)

Подставив значение (1.8) в формулу (1.7), получим

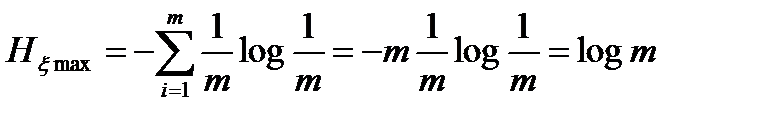, (1.9)

то есть H_xmax зависит только от числа символов в алфавите.

Теперь найдём минимальную энтропию. Отсутствие неопределён­ности характеризуется тем, что вероятность одного из символов, скажем x₁, равна единице р₁ = 1, а вероятность всех остальных сим­волов равна нулю: р₂=р₃=..,=р_m = 0. Подставив эти вероятности в формулу (1.7), получим

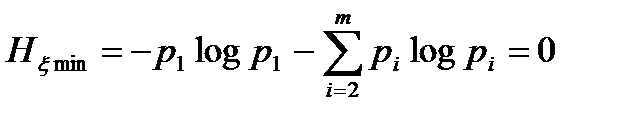, (1.10)

где для удобства анализа член, содержащий вероятность р₁,отделён от суммы. При p₁= 1 логарифм равен нулю: log₁ = 0. Поэтому первый член в целом равен нулю.

При р_i = 0, i =2,3,..., m член, содержащий сумму, также будет равен нулю. Говоря более точно, каждый член суммы соответствует неопределённости типа “ 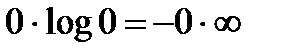”, раскрыв которую, получим нуль.

Таким образом, минимально возможная энтропия равна нулю; Н_xmin = 0. Это означает, что энтропия является положительной вели­чиной, заключённой в пределах

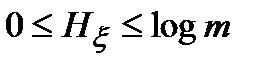. (1.11)

Энтропия (1.7), характеризующая среднее количество информа­ции, приходящейся на один символ алфавита, была получена в предпо­ложении, что появление любого символа алфавита полностью устра­няет неопределённость (1.5). Поэтому информация, определяемая формулой (1.7), иногда называется собственной информацией источ­ника сообщений, так как она определяет количество информации, приходящейся на один символ сообщения, без учета потерь в канале связи.