Эпсилон-энтропия непрерывного сообщения

Рассмотрим непрерывное сообщение в виде стационарного случайного процесса x(t) с известной одномерной плотностью вероят­ности р_x(х).

Проведём дискретизацию сообщения, для чего оп­ределим разрешённые уровни (х₁,x₂,...,x_m). Вероятность нахож­дения случайной величины на интервале 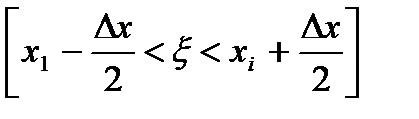в соответствии с процедурой квантования будем рассматривать как вероятность р_i того, что дискрет сообщения примет значение х_i, тогда при достаточно малом шаге квантования Dх будет иметь место равенство

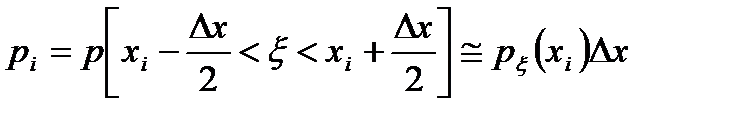. (2.4)

Квантование дискрета непрерывного сообщения позволяет заме­нить непрерывную функцию плотности вероятности сообщения p_x(x) рядом вероятности, у которого возможными значениями служат разрешённые уровни х₁, х₂,…х_m , а их соответствующие вероятности вычисляются по формуле (2.4).

Вышеприведённые предпосылки позволяют для определения энтропии непрерывного сообщения воспользоваться формулой (1.7), получен­ной для дискретного сообщения. Подставив (2.4) в формулу (1.7), получим

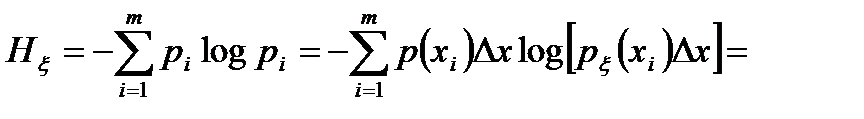
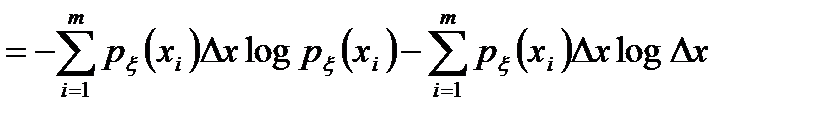, (2.5)

где воспользовались соотношением 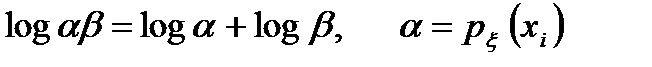, b=Dх. Если устремить Dx®dx, то суммирование в (2.5) заменится ин­тегрированием, которое распространим на всю числовую ось х. В то же время величину logDx, которая зависит от Dх и при его прибли­жении к нулю стремится к " 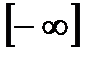", будем рассматривать как постоянную величину, не зависящую от х. В этом случае (2.5) примет вид

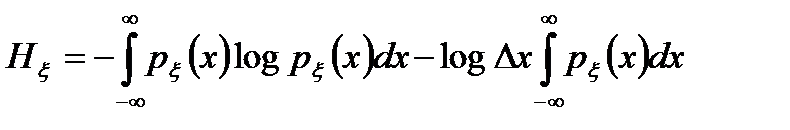. (2.6)

По условию нормировки плотности вероятности имеет место равенство

,

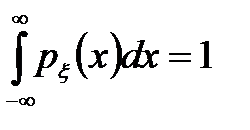то формулу (2.6) можно записать в виде

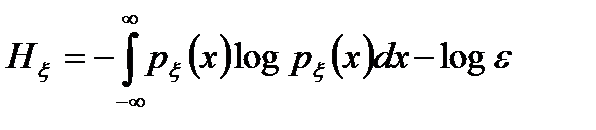, (2.7)

где 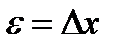- шаг квантования.

Из (2.7) следует, что энтропия непрерывного сообщения зави­сит как от плотности вероятности, так и от шага квантования. Причём при устремлении шага квантования к нулю теряется смысл выражения (2.7), так как

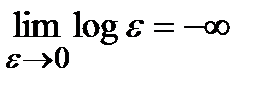. (2.8)

В литературе по теории информации величина (2,7) называется эпсилон-энтропией по названию буквы e, определяющей шаг квантования. Эпсилон-энтропию можно рассматривать как величину, определяющую среднее количество информации, приходящейся на один дискрет квантованного непрерывного сообщения.

Если конечные расчётные формулы представлять в виде разности энтропии, определяемых для одного и того же e, то log e будет вычитаться. Сказанное позволяет не учитывать log e (или условно рас­сматривать e= 1) и в качестве энтропии непрерывного сообщения использовать зависимость

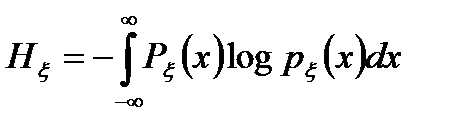, (2.9)

равную взятому со знаком минус математическому ожиданию логарифма плотности вероятности непрерывной случайной величины. В общем плане плотность вероятности р_x(х) является размерной величиной. Чтобы избежать некорректности, под логарифмом необходимо ставить р_x(х) в безразмерном виде, поделив её на единицу с размерностью плотности вероятности.

Энтропия (2.9) характеризует количество информации, приходя­щейся в среднем на один дискрет непрерывного сообщения. Если все дискреты на интервале [0, Т] являются независимыми случайными величинами, представляющими собой стационарный случайный процесс с одной и той же одномерной плотностью вероятности для всех своих сечений, то количество информации, заключённое в сообщении дли­тельностью Т, определяется выражением

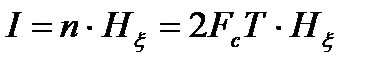. (2.10)

Формула (2.10) совпадает с выражением (2.16) для количества информации кодовой комбинации из n позиций в коде.