Информация на выходе канала связи

Рассмотрим дискретный канал связи. Пусть на его входе форми­руются дискретные сообщения с использованием алфавита из m симво­лов х₁, x₂, ..., x_m, вероятности которых равны р(x₁), р(х₂), ..., р(x_m). Рассматривая появление символа алфавита как реализацию случайной величины 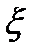можно найти энтропию сообщения на входе канала связи

, (3.1)

определяющую среднее количество информации, приходящейся на один символ входного сообщения.

Пусть в канале связи отсутствуют помехи. Тогда между символами на входе (x₁, x₂, ..., х_m) и выходе (y₁, y₂, ..., y_m) существует жёсткая связь. Это означает, что р(у₁) = р(x₁), p(y₂) = Р(х₂), .... р(y_m) = р(х_m) и энтропия на выходе

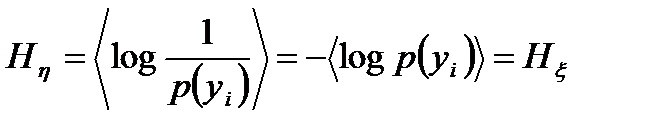(3.2)

равна энтропии на входе (рис. а).

Из (3.2) следует, что при отсутствии помех среднее количество информации, приходящейся на одни символ выходного сообщения, рав­но среднему количеству информации, приходящейся на один символ входного сообщения, при условии, что алфавиты входного и выходно­го сообщений совпадают.

Пусть в канале связи действуют помехи (рис. б). В этом случае появление символа у_j на выходе может быть не только под действием символа x_j на входе, но, вообще говоря, под действием любого х_i входного символа. Это возможно потому, что сигнал, соответствующий какому-либо входному символу, может быть так искажён, что на выходе он будет восприниматься как сигнал, соответствующий другому символу. В этом случае количество информации которое заключено в символе у_j, когда на входе действует символ х_i, определится по формуле

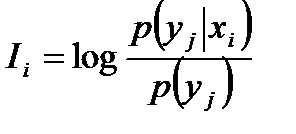, (3.3)

в которой p(y_j) соответствует вероятности появления символа у_j без учета действия помех. Так как в этом случае р(у_j) = P(x_j), то р(y_j) следует рассматривать как априорную вероятность Р₁ в форму­ле (3.1). В общем случае условная вероятность р(у_j|х₁) всегда меньше единицы :

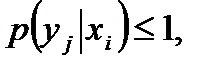
так как из точки х_i графа на рис. 18.1,б выходят ветви во все символы выходного алфавита и имеет место равенство

.

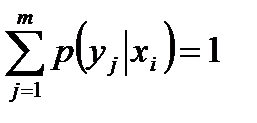Условную вероятность р(y_j|x_i) следует рассматривать как апостериорную вероятность Р₂ в формуле (3.1), считая, что 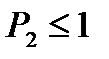то есть приход символа у_j не устраняет полностью имевшуюся ранее неопределённость о том, какой символ должен появиться.

Усреднив выражение (3.3) по всем возможным символам входного и выходного алфавита, то есть по всем i и j индексам, получим среднее количество информации, приходящееся на один символ сооб­щения на выходе канала связи:

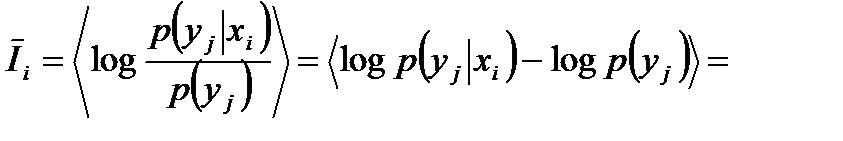
, (3.4)

где 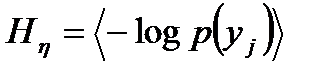- энтропия сообщения на выходе канала связи при отсутствии помех, - условная энтропия выходного сообщения, характеризующая действие помех.

Условная энтропия , всегда заключена в пределах

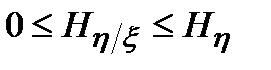. (3.5)

Действительно, если у_j и х_i жёстко связаны между собой, как это имеет место при отсутствии помех в канале связи (рис. а), то

.

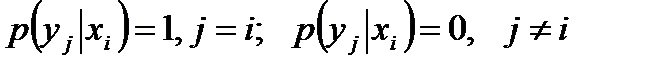В этом случае .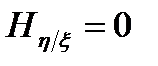

При сильной помехе, когда символы у_j возникают на приёмном конце связи независимо от посылаемых х_i, имеют место равенства:

.

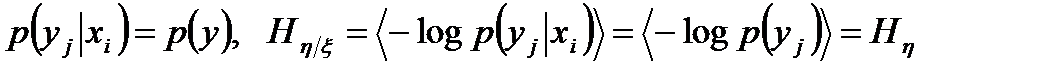Таким образом, при отсутствии помехи количество информации, приходящееся на один символ выходного сообщения, совпадает с энтропией входного сообщения

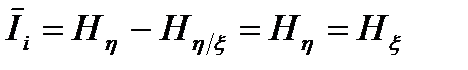. (3.6)

А при сильной помехе информация, заключённая в символе х_i, оказы­вается совершенно "размазанной" по всем символам у_j, так что в среднем выходной символ у_j никакой информации об х_i не несет и количество информации, которое в среднем приходится на один сим­вол сообщения у_j, равно нулю:

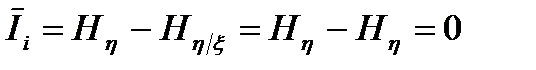. (3.7)

С уменьшением уровня помехи указанная "размазанность" умень­шается, что математически соответствует выполнению неравенства 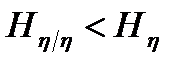. Поэтому в среднем по каналу связи один выходной символ передаёт информацию, определяемую выражением (3.4):

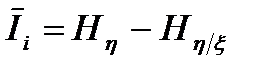. (3.8)

Это меньше, чем информация, заключенная в одном символе входного сообщения. Указанное уменьшение информации, обусловленное действием помехи, учитывает­ся условной энтропией .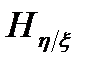

Заметим, что формулы (3.4), (3.5), (3.7), (3.8) в полной мере справедливы и для непрерывного канала связи. В теоретической литературе иногда количество информации, заключённое в символе у_j относительно символа х_i и определяемое формулой (3.8), называется взаимной информацией.