Кодирование сообщений в системах связи

При чтении какого-либо текста можно по смыслу найти и испра­вить неверно напечатанные, буквы. В теоретическом плане эта воз­можность основывается на наличии избыточности сообщения.

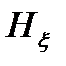Под избыточностью сообщения понимают разность между максимально возможной и реальной энтропией . Максимально возможная энтропия 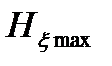определяется для случая, когда все символы дискретного сообщения равновероятны и независимы. Тогда при алфавите из m символов

.

Реальная энтропия H определяется для случая, когда символы алфа­вита имеют разную вероятность появления и, кроме того, в самом многопозиционном сообщении символы зависимы между собой.

Для характеристики избыточности сообщения используется коэффициент избыточности D, определяемый выражением

.

В русском алфавите 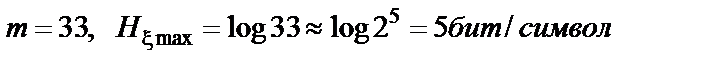. На самом деле буквы неравномерны и зависимы. Поэтому реальная энтропия русского языка составляет 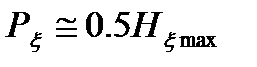. Коэффициент избыточности русского языка равен . Увеличение избыточности, приводящее к уменьшению , уменьша­ет скорость передачи информации и приводит, соответственно, к росту времени, необходимого на передачу одного и того же количества информации. В этом смысле избыточность играет отрицательную роль.

В то же время наличие избыточности позволяет создать коды с обнаружением и исправлением ошибок, обусловленных действием по­мех.

Поясним принцип создания кода с исправлением ошибок на основе использования избыточности.

Пусть требуется по каналу связи передать равновероятные сооб­щения "да" и "нет". В сообщении будет отсутствовать избыточность, если выбрать двоичный однопозиционный код (m = 2, n = 1), припи­сав "да" символу 1 и "нет" - символу 0. Энтропия кода будет равна 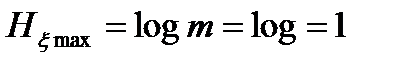бит/символ. В канале связи из-за действия помех может произойти замена или, как говорят, инвертирование символов с вероятностью ошибки Р_e = 0,1. Это означает, что с такой вероятностью обеспечивается прием передаваемого сообщения.

Теперь выбираем двоичный трёхпозиционный код (m = 2, n = 3), приписав "да" кодовой комбинации 111 и "нет" комбинации 000. В этом случае для передачи информации в 1 бит потребуется три сим­вола, Н = 1/3 бит/символ. Налицо избыточность, так как , что приводит к уменьшению скорости передачи информации в три раза и, соответственно, к увеличению в три раза времени, потребного для передачи одного сообщения. На приёмном конце наряду с комби­нациями 111, 000 могут возникнуть из-за действия помех комбинации 001, 010, 011, 100, 101, 110. Принимаемые кодовые комбинации, содержащие две или три единицы, будем воспринимать как сообщение "да", а принимаемые кодовые комбинации, содержащие два или три нуля, - как сообщение "нет". В этом случае инвертирование помехой одного символа комбинации не приводит к ошибке. Ошибка появляется лишь тогда, когда под действием помехи произойдет замена двух или трёх символов. Рассчитаем вероятность P_ош этой ошибки, пользуясь формулой Бернулли, когда число испытаний равно числу позиций в коде n = 3, вероятность осуществления собы­тия в одном испытании равно вероятности ошибки 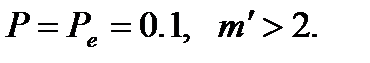Имеем

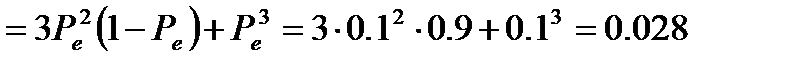
Заметим, что вероятность ошибки в трехпозиционном коде с избыточностью при вероятности инвертирования из-за помехи одного символа Р_е= 0.1 получилась приблизительно 0.1/0.028 3,5 раза меньше по сравнению с однопозиционным кодом без избыточности при том же уровне помех.