Классификация кодов

Применяемые в технике связи коды можно классифицировать по ряду специфических признаков.

По длине кодов и взаимному расположению в них символов различают равномерные и неравномерные коды.

Равномерные коды имеют одинаковую длину комбинаций. Для равномерного кода число возможных комбинаций составляет 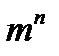. Примером такого кода является пятизначный код Бодо, применяемый в телеграфии. Код Бодо содержит пять двоичных элементов (m = 2, n = 5). Число возможных кодовых комбинаций в этом коде равно , что позволяет кодировать все буквы русского алфавита (твердый знак не передают). Однако этого мало для передачи сообщения на русском языке, содержащего буквы, цифры, знаки препинания и условные знаки (точка, запятая, двоеточие, сложение, вычитание, умножение и т. д.). Поэтому применяют «Международный код №2» (МТК-2). В коде МТК-2 используется регистровый принцип, согласно которому одна и та же пятиэлементная кодовая комбинация может использоваться до трех раз в зависимости от положения регистра: русский, латинский, цифровой. Общее число различных знаков при этом равно 84, что достаточно для кодирования телеграммы.

Неравномерные коды отличаются тем, что кодовые комбинации у них отличаются друг от друга не только взаимным расположением символов, но и их количеством при минимизации средней длины кодовой последовательности. Это приводит к тому, что различные комбинации имеют различную длительность.

Общая идея построения неравномерных кодов подсказывается теоремой кодирования 1 Шеннона для каналов без помех. Очевидно, что средняя длина неравномерного кода будет минимизироваться тогда, когда с более вероятными сообщениями источника будут сопоставляться более короткие комбинации канальных символов. Однако проблема заключается в том, что у неравномерного кода на приемной стороне оказываются неизвестными границы этих комбинаций. Если же попытаться их выделить, используя известный способ кодирования, то декодирование может оказаться неоднозначным (действительно, если, например, букве А присвоена комбинация 1, букве Б - 0, а букве В - 10, то невозможно определить по принятой комбинации 10, передавались ли буква В или пара букв А и Б). Для того, чтобы используемый код был однозначно декодируемым, он должен удовлетворять некоторым условиям. Однозначное декодирование будет обеспечено, если ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие этим условиям, называются префиксными или неприводимыми. Кстати, равномерный код также является префиксным.

Наиболее известным неравномерным кодом является код Морзе, в котором символы 1 и 0 используется в двух сочетаниях - как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, отражающий одну единицу, соответствует точке («.»), трем единицам – тире («-»). Символ 0 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как разделительный знак между кодовыми комбинациями.

По признаку помехозащищенности коды, как и методы кодирования, делят на примитивные (первичные, простые, безызбыточные) и помехоустойчивые (корректирующие, избыточные).

Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются примитивными или кодами без избыточности. В простых равномерных кодах превращение одного символа комбинации в другой, например 0 в 1 или 1 в 0, приводит к появлению новой разрешенной комбинации, т.е. к ошибке в принятом сообщении.

Примитивное, или безызбыточное, кодирование применяется для согласования алфавита источника и алфавита канала. Отличительное свойство примитивного кодирования состоят в том, что избыточность дискретного источника, образованного выходом примитивного кодера, равна избыточности источника на входе кодера. Примитивное кодирование используется также в целях шифрования передаваемой информации для ее защиты от несанкционированного доступа и повышения устойчивости работы устройств синхронизации систем связи.

В помехоустойчивых кодах для передачи сообщения используются не все кодовые комбинации, а только некоторая их часть (разрешенные кодовые комбинации). Тем самым создается возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов обеспечиваются введением в кодовые комбинации дополнительных (избыточных) символов.

В настоящее время разработано большое число помехоустойчивых кодов, которые могут быть классифицированы по различным признакам.

По способу кодирования помехоустойчивые коды обычно разбивают на два класса: блочные и непрерывные.

Блочное кодирование состоит в том, что последовательность символов источника сообщений (последовательность нулей и единиц) разделяется на блоки, которые обычно называют кодовыми комбинациями. На практике количество символов в блоке может быть в пределах от 3 до нескольких сотен.

Блоки, содержащие k символов каждый, по определенному закону преобразуются кодером в n-символьные блоки, причем n > k. Например, схема блочного кодера

Каждый символ выходного блока информации получается как сумма по модулю 2 нескольких символов входного блока, для чего используются n сумматоров по модулю 2. Совокупность всех возможных кодовых комбинаций при блочном способе кодирования, и есть блочный код.

Непрерывные коды характеризуются тем, что кодирование и декодирование информационной последовательности символов осуществляется без ее разбиения на блоки. Каждый символ выходной последовательности получается как результат некоторых операций над символами входной последовательности. Кодирование и декодирование непрерывных кодов носит непрерывный характер. При этом результат декодирования предыдущих или последующих символов может повлиять на декодирование текущего символа. Среди непрерывных кодов наиболее часто применяют сверточные коды.

Блочные коды подразделяются на разделимые и неразделимые. К разделимым относятся коды, кодовые комбинации которых состоят из двух частей: информационной и проверочной. Обычно проверочные символы получаются посредством некоторых операций над информационными символами. Разделимые коды условно обозначают в виде (n, k), где n – число символов в кодовой комбинации, k – число информационных символов. Число проверочных символов в разделимых блочных кодах равно r = n-k.

К неразделимым относятся коды, кодовые комбинации которых нельзя разделить на информационные и проверочные части.

Самый большой класс разделимых кодов составляют систематические коды, у которых значения проверочных символов определяются в результате проведения линейных операций над информационными символами. Последовательность линейных операций и число проверочных символов определяется тем, сколько ошибок должен исправлять и обнаруживать данный код. Проверочные символы могут располагаться на любом месте кодовой комбинации. Однако обычно проверочные символы записывают к информационным символам справа, т.е. располагают на месте младших разрядов.

Например, рассмотрим схему наиболее простого систематического кодера (5,4). Здесь всего лишь один проверочный символ формируется из информационных символов путем их суммирования по модулю 2. Этот код называют кодом с проверкой на четность. Так как новую разрешенную комбинацию систематического кода можно получить линейными преобразованиями двух разрешенных, то такие коды часто называют линейными или групповыми.

К несистематическим (нелинейным) относятся коды, в которых проверочные символы формируются за счет некоторых нелинейных операций над информационными символами. Примером нелинейного кода является код Бергера.

4.4 Основные характеристики помехоустойчивых кодов

Основными характеристиками помехоустойчивых кодов являются:

1. Длина кода n – это число символов в кодовой комбинации. Например, комбинация 11010 состоит из пяти символов, следовательно, n=5. Если все кодовые комбинации содержат одинаковое число символов, то код называется равномерным. В неравномерных кодах длина кодовых комбинаций может быть разной.

2. Основание кода m – это число различных символов в коде. Для двоичных кодов символами являются 1 и 0, поэтому m=2.

3. Число кодовых комбинаций для равномерного кода равно N=mⁿ. Например, для равномерного двоичного кода, имеющего длину n=6, число различных кодовых комбинаций равно N=2⁶=64.

4. Число разрешенных кодовых комбинаций N_р – это количество кодовых комбинаций кода, используемых для передачи сообщений. Для помехоустойчивых кодов N_р<N. Оставшиеся кодовые комбинации N-N_р называют запрещенными. Если N_р=N, то код является безызбыточным. Для разделимых кодов N_р=2 ^k.

5. Избыточность кода К_и в общем случае определяется выражением

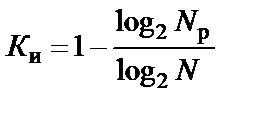
и показывает, какая доля длины кодовой комбинации не используется для передачи информации, а используется для повышения помехоустойчивости кода. Для разделимых кодов

,

где величина k/n называется относительной скоростью кода.

6. Кодовое расстояние d(А,В) – это число позиций, в которых две кодовые комбинации А и В отличаются друг от друга. Например, если А=01101, В=10111, то d(А,В)=3. Кодовое расстояние между комбинациями А и В может быть найдено в результате сложения по модулю 2 одноименных разрядов комбинаций, а именно

,

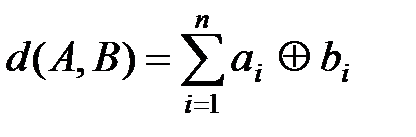где a_i и b_i – i-е разряды кодовых комбинаций A и B; символ Å обозначает сложение по модулю 2.

Кодовое расстояние между различными комбинациями конкретного кода может быть различным. Так, для первичных кодов это расстояние для различных пар кодовых комбинаций может принимать значения от единицы до величины длины кода.

7. Минимальное кодовое расстояние d_min – это минимальное расстояние между разрешенными кодовыми комбинациями данного кода. Минимальное кодовое расстояние является основной характеристикой корректирующей способности кода. В первичных (безызбыточных) кодах все комбинации являются разрешенными, поэтому минимальное кодовое расстояние для них равно единице (d_min=1). Такие коды не способны обнаруживать и исправлять ошибки. Для того чтобы код обладал корректирующими способностями, его минимальное кодовое расстояние должно быть не менее двух (d_min ³ 2).

Для обнаружения всех ошибок кратностью s и менее, минимальное кодовое расстояние должно удовлетворять условию

d_min ³ s +1 .

Если код используется для исправления ошибок кратности не более t, то минимальное кодовое расстояние должно иметь значение

d_min ³ 2t +1.

Под кратностью ошибки понимается число позиций кодовой комбинации, в которых под воздействием помех одни символы оказались замененными другими (нули – единицами, единицы - нулями).

Для обнаружения s ошибок и исправления t ошибок должно выполняться условие

d_min ³ s + t +1 .

Таким образом, задача построения кода с заданной корректирующей способностью сводится к обеспечению необходимого кодового расстояния. Увеличение d_min приводит к росту избыточности кода. При этом желательно, чтобы число проверочных символов r было минимальным. В настоящее время известен ряд верхних и нижних границ, которые устанавливают связь между кодовым расстоянием и числом проверочных символов.

МОДУЛЯЦИЯ СИГНАЛОВ