Теоремы кодирования для каналов без помех и с помехами

Рассмотрим дискретный канал связи без помех. Пусть источник сообщения характеризуется производительностью

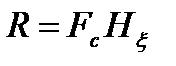бит/с,

где F_с - средняя частота появления символа в единицу времени; 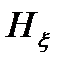- энтропия сообщения.

В свою очередь, дискретный канал связи без помех характеризу­ется пропускной способностью, определяемой наибольшей возможной скоростью передачи информации в канале, когда условная энтропия равна нулю

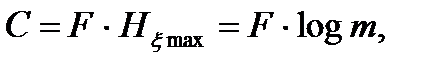бит/с ,

где m - число символов в алфавите сообщения; F - полоса пропускания канала.

В общем плане согласование источника сообщений с каналом сос­тоит не в том, чтобы обеспечить согласование F_с с F, а в том, чтобы обеспечить согласование R с С.

Существует теорема Шеннона для дискретного канала связи без помех. Если пропускная способность канала превышает производительность источника сообщений, то есть выполняется усло­вие

,

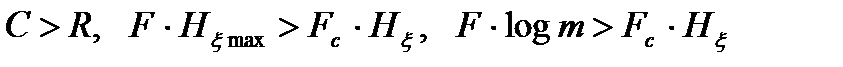то существует такой способ кодирования сообщения, при котором скорость передачи информации в канале R будет сколь угодно близ­кой к пропускной способности канала С. Если условие не выполняется, то такого способа кодирования нет.

Если рассматривается дискретный канал связи с помехами, то его пропускная способность определяется выраже­нием

.

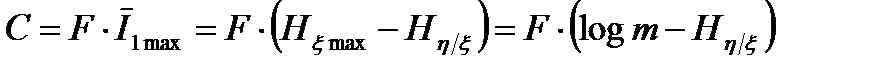Существует вторая теорема Шеннона. Для дискретного канала связи с помехами существует такой способ кодирования, при котором может быть обеспечена безошибочная передача всей информа­ции, поступающей от источника сообщений, если только пропускная способность канала превышает производительность источника сообще­ний, то есть выполняется условие

C > R .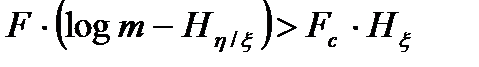

Если условие не выполняется, то способа кодирования, обеспечивающего сколь угодно малую вероятность ошибки, не сущест­вует.

Приведенные теоремы Шеннона играют роль предельных теорем. Они указывают на возможность достижения необходимого кодирования, но не позволяют сформулировать сам способ кодирования. Однако эти теоремы послужили толчком к бурному развитию прикладной теории кодирования.

Теория кодиро­вания развивается в двух главных направлениях: во-первых, поиски кодов, позволяющих в каналах без помех максимально устранить из­быточность источника и тем самым повысить скорость передачи ин­формации. Этим занимается теория экономического кодирования. Её теоретической основой является первая теорема Шеннона. Во-вторых, поиски кодов, повышающих достоверность передачи информации в ка­налах с помехами. Этим занимается теория помехоустойчивого коди­рования. Её теоретической основой является вторая теорема Шенно­на.

Практическая реализация кодирования на передающей стороне всегда предполагает применение обратной процедуры – декодирования – для восстановления принятого сообщения. Устройства, осуществляющие кодирование и декодирование, называются соответственно кодер и декодер. Выполняются они обычно в одной микросхеме и образуют устройство, называемое кодеком.