Радиосигналы с частотной модуляцией

При частотной модуляции частота несущего колебания меняется в такт передаваемому сообщению s(t)

,

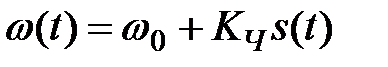Здесь 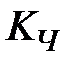– размерный коэффициент пропорциональности между частотой и напряжением, рад/(В×с)

Рассмотрим однотональную частотную модуляцию, в этом случае:

.

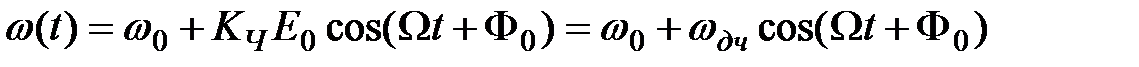Здесь 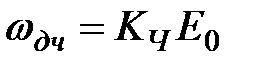– девиация частоты сигнала (наибольшее отклонение мгновенной частоты модулированного радиосигнала при частотной модуляции от значения его несущей частоты).

Полная фаза ЧМ-сигнала в любой момент времени определяется путем интегрирования частоты:

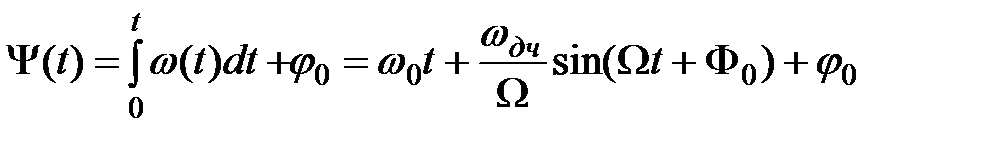
Величина 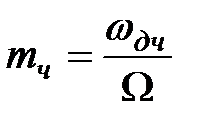называется индексом частотной модуляции. Положим для простоты 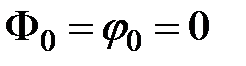и выразим мгновенное значения ЧМ- сигнала в виде

.

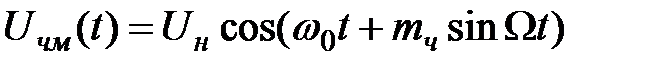Рассмотрим два случая: 1) 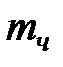<< 1; 2) 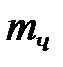> 1.

Рассмотрим вначале первый случай ( 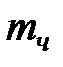<< 1 ).

Поскольку 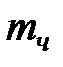мало, можно принять, что ; » .

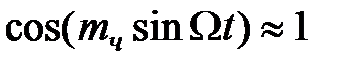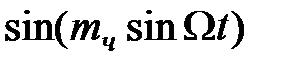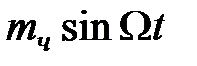Тогда

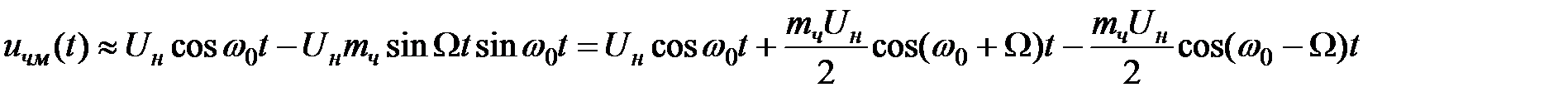Таким образом, в спектре ЧМ-сигнала при 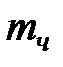<< 1 содержится несущее колебание 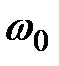и два боковых колебания 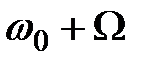и 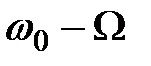, как и в случае АМ- сигнала. Однако, в отличие от АМ, нижнее боковое колебание имеет дополнительный фазовый сдвиг на .

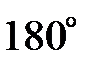В энергетическом отношении частотная модуляция с 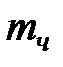<< 1 крайне неэффективна, т.к. мощность обоих боковых колебаний очень мала.

Рассмотрим второй случай 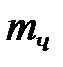> 1. Данный случай представляет основной практический интерес, поскольку при больших 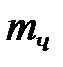помехоустойчивость передачи сигнала существенно выше, чем при амплитудной модуляции. Здесь при расчетах оказывается удобным аппарат функций Бесселя. Можно показать, что в этом случае ЧМ-сигнал представляется в виде:

где 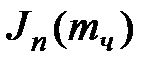- функция Бесселя n-ого индекса от аргумента .

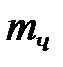Спектр ЧМ-сигнала с однотональной модуляцией при индексе модуляции 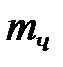> 1 состоит из трех высокочастотных гармоник: исходного несущего колебания и бесконечного числа боковых составляющих с частотам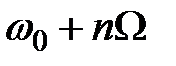и и 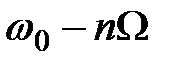расположенными попарно и симметрично относительно несущей частоты .

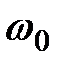Теоретически, спектр ЧМ-сигнала (аналогично и ФМ-сигнала) бесконечен по полосе частот, однако коэффициенты при n ³ 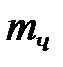+ 1 становятся такими малыми, что ими можно пренебречь.

Поэтому считается, что практическая ширина спектра радиосигналов с угловой модуляцией

.

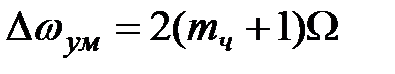ЧМ- и ФМ-сигналы, применяемые в практических схемах, имеют индекс модуляции 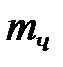>> 1, поэтому

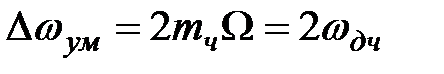
Таким образом, полоса частот, занимаемая сигналами с однотональной частотной модуляцией, равна удвоенной величине девиации частоты и не зависит от частоты модуляции.