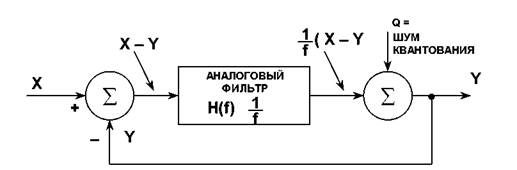
УПРОЩЕННАЯ ЛИНЕАРИЗИРОВАННАЯ МОДЕЛЬ SIGMA-DELTA МОДУЛЯТОРА В ЧАСТОТНОЙ ОБЛАСТИ

Y = 1 ( X - Y ) + Q ПЕРЕНОСЯ И РЕШАЯ УРАВНЕНИЕ ОТНОСИТЕЛЬНО Y ПОЛУЧАЕМ:

Y = f X 1 + Q f

/ \

СИГНАЛЬНАЯ СОСТАВЛЯЮЩАЯ ШУМОВАЯ СОСТАВЛЯЮЩАЯ

Рис. 3.13

Интегратор в Σ∆-модуляторе представлен в виде аналогового ФНЧ с передаточной функцией H(f) = 1/f. Эта передаточная функция имеет обратную входному сигналу амплитудную характеристику. Одноразрядный источник импульсов генерирует шум квантования Q, который добавляется к выходному сигналу суммирующего блока. Если считать входной сигнал равным X, а выходной - равным Y, то сигнал на выходе входного сумматора должен быть X - Y. Эта величина умножается на передаточную функцию фильтра 1/f, и результат подается на один из входов выходного сумматора. В итоге получается выражение для выходного напряжения Y в виде:

Y = —(X - Y ) + Q f

Это выражение может быть легко решено относительно Y c аргументами X, f и Q:

Y =

X Q ⋅ f

f+1 f+1

Обратите внимание, что, когда частота f приближается к нулю, значение выходного напряжения Y стремится к X, а шумовая составляющая устремляется к нулю. На более высоких частотах амплитуда сигнальной составляющей стремится к нулю, а шумовая составляющая приближается к Q. При дальнейшем повышении частоты выходной сигнал состоит практически из одного шума квантования. В сущности, аналоговый фильтр представляет собой ФНЧ для сигнала и ФВЧ для шума квантования. Иными словами, аналоговый фильтр выполняет функцию формирования кривой распределения шума квантования в модели Σ∆-модулятора.

При фиксированной входной частоте аналоговый фильтр дает тем большее затухание, чем выше порядок этого фильтра. Это же положение с определенным допущением справедливо для Σ∆-модуляторов.

С ростом числа каскадов интегрирования и суммирования в Σ∆-модуляторе достигается лучший эффект при формировании кривой распределения шума квантования и лучшее эффективное число разрядов (ENOB) при фиксированном коэффициенте избыточной дискретизации, как это следует из рис.3.14 для Σ∆-модуляторов первого-второго порядков. Блок-схема Σ∆-модулятора второго порядка представлена на рис.3.15. До недавнего времени считалось, что Σ∆ АЦП третьего и более высокого порядков должны быть потенциально нестабильными при определенных входных сигналах. Последние исследования, рассматривающие компараторы c конечным, а не с бесконечным коэффициентом усиления, показали несостоятельность этого предположения. Даже если и существует неустойчивость, она не вносит существенной погрешности, так как цифровой сигнальный процессор (DSP) цифрового фильтра и дециматор в состоянии распознать возникающую неустойчивость и предотвратить ее.

На рис.3.16 показаны соотношения между порядком Σ∆-модулятора и уровнем избыточной дискретизации, необходимым для достижения требуемого отношения сигнал/шум (SNR). В частности, если коэффициент избыточной дискретизации равен 64, идеальная система второго порядка способна обеспечить отношение сигнал/шум на уровне 80 дБ. Этим подразумевается, что значение эффективного числа разрядов (ENOB) равное приблизительно 13. Хотя фильтрация, выполняемая цифровым фильтром и дециматором, может приводить к любой желаемой степени точности, нет смысла выводить более 13 двоичных разрядов. Дополнительные разряды не дадут никакой полезной информации о сигнале, и информация будет подавлена шумом квантования, если не использовать дополнительной фильтрации. Повышенная разрешающая способность может быть достигнута за счет увеличения коэффициента избыточной дискретизации и/или за счет использования модулятора более высокого порядка.