Адаптивные системы с моделью
Эффективным способом поддержания экстремального режима адаптивной системы является введение в контур самонастройки эталонной модели. В этом случае процессы, протекающие в эталонной модели (модели – эталоне), соответствуют заданным экстремальным условиям качества.
Сравнивая динамические процессы реального объекта с процессами в модели, можно подстраивать характеристики системы управления таким образом, чтобы приближать процесс реального объекта к процессу модели, обеспечивая таким образом функционирование реальной системы в экстремальном режиме.
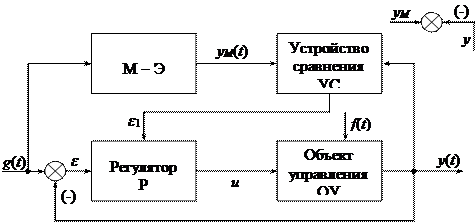
Рассмотрим блок-схему адаптивной системы с моделью-эталоном М-Э.
В зависимости от ошибки e1(t) изменяются параметры регулятора.
Уравнения адаптивной системы с эталонной моделью можно записать так
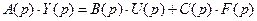
| – уравнение ОУ. |
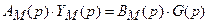
| – уравнение ЭМ. |
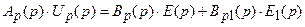
| – уравнение регулятора. |
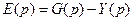
| – уравнение сумматора основного контура. |
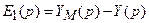
| – уравнение сумматора контура адаптации. |
Здесь g(t) – задающее воздействие, которое измеряется, но изменяться может произвольным образом.
f(t) – возмущение, приложенное к объекту, которое не измеряется, а изменяться может произвольным образом.
 |
Поскольку процесс y(t) должен отслеживать процесс YM(t), то это означает, что решения уравнений ОУ и ЭМ должны быть близкими друг к другу.
Это возможно в двух случаях:
− когда уравнения ОУ и ЭМ идентичны, начальные условия одинаковы и воздействия, приложенные к ОУ и ЭМ, также одинаковы.
Этот случай невозможен, так как параметры ОУ могут меняться, возмущение f приложено только к ОУ и заранее неизвестно, и входные воздействия к ОУ и ЭМ принципиально различны.
− второй случай, когда и математические модели отличаются и начальные условия разные и воздействия разные, однако за счет управляющих воздействий, определяемых ошибками 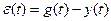 и
и 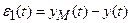 удается так корректировать динамику ОУ, что
удается так корректировать динамику ОУ, что 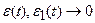 .
.
Выразим правую часть уравнения ОУ через сигналы ошибок E(p)и E1(p). Поскольку рассматриваются стационарные объекты и модели будем иметь:
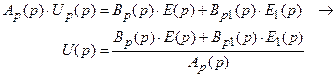
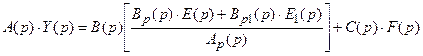 (*)
(*)
Анализ выражения (*). Правая часть уравнения (*) зависит от неконтролируемого воздействия F(p) и двух измеряемых воздействий E(p)и E1(p).
− Чем больше ошибки E(p)и E1(p), тем в большей степени эти переменные будут оказывать влияние на выходную координату объекта управления Y(p). Операторы 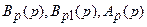 должны выбираться таким образом, чтобы с возрастанием E(p)и E1(p) выходная координата Y(p) изменялась бы таким образом, чтобы эти ошибки уменьшались, в противном случае система будет неработоспособной. Здесь много будет зависеть от величины и знака возмущения F(p).
должны выбираться таким образом, чтобы с возрастанием E(p)и E1(p) выходная координата Y(p) изменялась бы таким образом, чтобы эти ошибки уменьшались, в противном случае система будет неработоспособной. Здесь много будет зависеть от величины и знака возмущения F(p).
− Даже в случае достижения условия 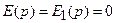 уравнение вырождается таким образом:
уравнение вырождается таким образом:
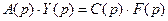 ,
,
а так как F(p) изменяется неконтролируемым образом, то процесс изменения Y(p) будет носить всегда переходный характер.
− Контур с ЭМ влияет на устойчивость системы в целом.
Дата добавления: 2015-12-11; просмотров: 2309;
