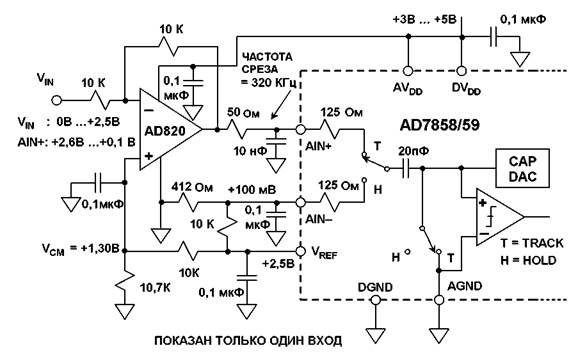
ПОДКЛЮЧЕНИЕ ВХОДА С КОММУТИРУЕМЫМ
КОНДЕНСАТОРОМ
12-РАЗРЯДНОГО 200KSPS АЦП AD7858/59
Sigma-delta (Σ∆) АЦП Джеймс Брайэнт
Sigma-delta АЦП известны почти тридцать лет, но только недавно появилась технология (цифровые микросхемы с очень высокой степенью интеграции, VLSI) для их производства в виде недорогих монолитных интегральных схем. В настоящее время они используются во многих приложениях, где требуется недорогой, узкополосный, экономичный АЦП с высоким разрешением.
Существуют многочисленные описания архитектуры и теории Σ∆ АЦП, но большинство из них переполнено сложными интегральными выражениями и с трудом доступно для понимания. В отделе по приложениям компании Analog Devices мы часто сталкиваемся с инженерами, которые не понимают теории работы Σ∆ АЦП и убеждены на опыте чтения распространенных статей, что Σ∆ АЦП слишком сложны для понимания.
Не прибегая к глубоким математическим выкладкам, заметим, что в понимании sigma-delta АЦП нет ничего особенно трудного, и данный раздел призван подтвердить это положение.. Σ∆ АЦП содержит очень простую аналоговую электронику (компаратор, источник опорного напряжения, коммутатор и один или большее количество интеграторов и аналоговых сумматоров) и весьма сложную цифровую вычислительную схему. Эта схема состоит из цифрового сигнального процессора (DSP), который работает
как фильтр (в общем случае, но не всегда — это низкочастотный полосовой фильтр). Нет необходимости в точности знать, как работает фильтр, чтобы понимать то, что он делает. Для понимания того, как работает Σ∆ АЦП, важно познакомиться с концепциями избыточной дискретизации, формирования формы кривой распределения шума квантования, цифровой фильтрации и децимации.
CИГМА-ДЕЛЬТА АЦП
■ Низкая стоимость, высокая разрешающая способность (до 24-разрядов)
■ Превосходная дифференциальная нелинейность (DNL)
■ Низкая потребляемая мощность, но ограниченная полоса пропускания (голосовые и звуковые частоты)
■ Простые ключевые концепции, но сложная математика
♦ Избыточная дискретизация
♦ Формирование шума квантования
♦ Цифровая фильтрация
♦ Децимация
■ Идеален для устройств обработки сигналов датчиков
♦ Высокая разрешающая способность
♦ Режимы: автономный, системный и автокалибровки
■ Широко применяется в области обработки голосовых и аудио
сигналов
Рис. 3.10
Рассмотрим методику избыточной дискретизации с анализом в частотной области. Там, где преобразование постоянного напряжения имеет ошибку квантования до ½ младшего разряда (LSB), дискретная система, работающая с переменным напряжением или током, обладает шумом квантования. Идеальный классический N-разрядный АЦП имеет среднеквадратичное значение шума квантования, равное q/√12. Шум квантования равномерно распределен в пределах полосы Найквиста от 0 до fs/2 (где q — значение младшего значащего бита и fs — частота дискретизации), как показано на рис.3.11 а. Поэтому, его отношение сигнал/шум для полнодиапазонного синусоидального входного сигнала будет (6,02N+1,76)дБ.. Если АЦП несовершенен и его реальный шум больше, чем его теоретический минимальный шум квантования, то эффективная разрешающая способность будет меньше, чем N-разрядов. Его фактическая разрешающая способность (часто известная как эффективное число разрядов или ENOB) будет определена, как
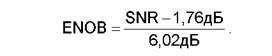
Если мы выберем более высокую частоту дискретизации K fs (см. рис.3.11 б), то среднеквадратичное значение шума квантования остается q/√12, но шум теперь распределен по более широкой полосе от 0 до fs /2. Если мы затем используем на выходе цифровой низкочастотный фильтр, то значительно уменьшим шум квантования, но сохраним полезный сигнал, улучшая таким способом эффективное число разрядов (ENOB). Таким образом, мы выполняем аналого-цифровое преобразование с высоким
разрешением, используя аналого-цифровой преобразователь с низкой разрешающей способностью. Коэффициент K здесь упоминается, как коэффициент избыточной дискретизации. При этом необходимо отметить, что избыточная дискретизация дополнительную выгодна еще и тем, что она понижает требования к аналоговому ФНЧ.
Дата добавления: 2016-01-07; просмотров: 959;
