Скрытие данных в частотной области изображения

Как уже было отмечено выше, стеганографические методы скрытия данных в пространственной области изображения являются нестойкими к большинству из известных видов искажений. Так, например, использование операции компрессии с потерями (относительно изображения, это может быть JPEG-компрессия) приводит к частичному или, что более вероятно, полному уничтожению встроенной в контейнер информации. Более стойкими к разнообразным искажениям, в том числе и компрессии, являются методы, использующие для скрытия данных не пространственную область контейнера, а частотную.

Существует несколько способов представления изображения в частотной области.

Наибольшее распространение среди всех ортогональных преобразований в стеганографии получили вейвлет-преобразования и ДКП [22], что определенной мерой объясняется значительным распространением их использования при компрессии изображений. Кроме того, для скрытия данных целесообразно применять именно то преобразование изображения, которому последнее будет подвергаться со временем при возможной компрессии. Например, известно, что алгоритм ДКП является базовым в стандарте JPEG, а вейвлет-преобразования – в стандарте JPEG2000.

Структурная схема стеганосистемы приведена на рисунке 11.4.

Рисунок 11.4 - Структурная схема стеганосистемы при наличии в стеганоканале атаки компрессии

Первичное изображение С раскладывается на D субполос (прямое преобразование), в каждую из которых встраивается скрываемая информация М. После обратного преобразования получается модифицированное изображение S.После компрессии/декомпрессии Θ в канале связи получается изображение
S 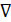, которое на принимающей стороне вновь подвергается прямому преобразованию и из каждой субполосы D независимо извлекается скрытое сообщение – оценка М.

Известно, и данный факт используется в алгоритмах компрессии, что большая часть энергии изображений сосредоточена в низкочастотной (НЧ) области спектра. Отсюда и возникает необходимость в осуществлении декомпозиции изображения на субполосы, к которым прибавляется стеганособщение. НЧ субполосы содержат основную часть энергии изображения и, таким образом, носят шумовой характер. Высокочастотные (ВЧ) субполосы спектра изображения наибольшим образом поддаются влиянию со стороны разнообразных алгоритмов обработки, таких как, например, компрессия или НЧ-фильтрация. Таким образом, можно сделать вывод, что для встраивания сообщения самыми оптимальными являются среднечастотные (СЧ) субполосы спектра изображения.

Во время цифровой обработки изображения часто применяется двумерная версия дискретного косинусного преобразования:

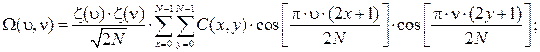(11.1)

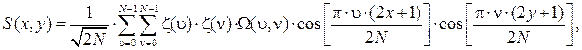(11.2)

где C(x, у) и S{x, у)– соответственно, элементы оригинального и восстановленного по коэффициентам ДКП изображения размерностью NxN; х,у – пространственные координаты пикселей изображения; Ω(υ,ν) – массив коэффициентов ДКП; υ,ν – координаты в частотной области; 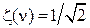,если ν= 0 и ζ(ν) = 1, если ν > 0.

Рассмотрим существующие методы, которые базируются на алгоритме ДКП.

11.4.2.1 Метод относительной замены величин коэффициентов ДКП (метод Коха и Жао).Один из наиболее распространенных на сегодня методов скрытия конфиденциальной информации в частотной области изображения заключается в относительной замене величин коэффициентов ДКП[21].

На начальном этапе первичное изображение разбивается на блоки размерностью 8×8 пикселей. ДКП применяется к каждому блоку – формула (11.1), в результате чего получают матрицы 8×8 коэффициентов ДКП, которые зачастую обозначают Ω_b(υ,ν), где b – номер блока контейнера С, a (υ,ν)– позиция коэффициента в этом блоке. Каждый блок при этом предназначен для скрытия одного бита данных.

Было предложено две реализации алгоритма: псевдослучайно могут выбираться два или три коэффициента ДКП. Рассмотрим первый вариант.

Во время организации секретного канала абоненты должны предварительно договориться о двух конкретных коэффициентах ДКП из каждого блока, которые будут использоваться для скрытия данных. Зададим данные коэффициенты их координатами в массивах коэффициентов ДКП: (υ₁,ν₁) и (υ₂, ν₂). Кроме этого, указанные коэффициенты должны отвечать косинус-функциям со средними частотами, что обеспечит скрытость информации в существенных для ЗСЧ областях сигнала, к тому же информация не будет искажаться при JPEG-компрессии с малым коэффициентом сжатия.

Непосредственно процесс скрытия начинается со случайного выбора блока С_ь изображения, предназначенного для кодирования b-го бита сообщения. Встраивание информации осуществляется таким образом: для передачи бита "0"стремятся, чтобы разница абсолютных значений коэффициентов ДКП превышала некоторую положительную величину, а для передачи бита "1" эта разница делается меньшей по сравнению с некоторой отрицательной величиной:

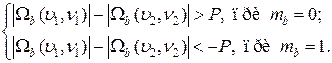(11.3)

Таким образом, первичное изображение искажается за счет внесения изменений в коэффициенты ДКП, если их относительная величина не отвечает скрываемому биту. Чем больше значение P тем стеганосистема, созданная на основе данного метода, является более стойкой к компрессии, однако качество изображения при этом значительно ухудшается.

После соответствующего внесения коррекции в значения коэффициентов, которые должны удовлетворять неравенству (11.3), проводится обратное ДКП.

Для извлечения данных, в декодере выполняется аналогичная процедура выбора коэффициентов, а решение о переданном бите принимается в соответствии со следующим правилом:

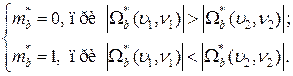(11.4)

11.4.2.2 Метод Бенгама-Мемона-Эо-Юнг.Бенгам (D. Benham), Мемон (N. Метоп), Эо (B.-L. Yeo) и Юнг (Minerva Yeung) [29] предложили оптимизированную версию вышерассмотренного метода. Причем оптимизация была проведена ими по двум направлениям: во-первых, было предложено для встраивания использовать не все блоки, а только наиболее подходящие для этого, во-вторых, в частотной области блока для встраивания выбираются не два, а три коэффициента ДКП, что, как будет показано в дальнейшем, существенно уменьшает визуальные искажения контейнера. Рассмотрим отмеченные усовершенствования более подробно.

Пригодными для встраивания информации считаются такие блоки изображения, которые одновременно удовлетворяют следующим двум требованиям:

-блоки не должны иметь резких переходов яркости;

-блоки не должны быть слишком монотонными.

Блоки, которые не отвечают первому требованию, характеризуются наличием слишком больших значений низкочастотных коэффициентов ДКП, сопоставимых по своей величине с DC-коэффициентом. Для блоков, которые не удовлетворяют второму требованию, характерно равенство нулю большинства высокочастотных коэффициентов. Указанные особенности являются критерием отбраковки непригодных блоков.

Отмеченные требования отбраковки учитываются использованием двух пороговых коэффициентов: P_L (для первого требования) и Р_H (для второго требования), превышение (P_L) или недостижение (Р_H) которых будет указывать на то, что рассматриваемый блок не пригоден для модификации в частотной области.

Встраивание в блок бита сообщения совершается следующим образом. Выбираются (для большей стойкости стеганосистемы – псевдослучайно) три коэффициента ДКП блока из среднечастотной области с координатами (υ₁,ν₁), (υ₂, ν₂) и (υ₃, ν₃). Если необходимо провести встраивание «0», эти коэффициенты изменяются таким образом (если, конечно, это необходимо), чтобы третий коэффициент стал меньше любого из первых двух; если необходимо скрыть «1», он делается большим по сравнению с первым и вторым коэффициентами:

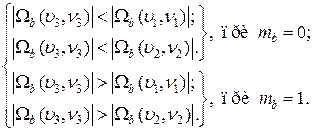(11.5)

Как и в предыдущем методе, для принятия решения о достаточности различения указанных коэффициентов ДКП, в выражение (11.5) вводится значение порога различения Р:

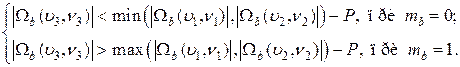(11.6)

В том случае, если такая модификация приводит к слишком большой деградации изображения, коэффициенты не изменяют, и блок в качестве контейнера не используется.

Использование трех коэффициентов вместо двух и, что самое главное, отказ от модификации блоков изображения в случае неприемлемых их искажений, уменьшает погрешности, которые вносятся сообщением. Получатель всегда может определить блоки, в которые не проводилось встраивание, просто повторив анализ, аналогичный выполненному на передающей стороне.

11.4.2.3 Метод Хсу и By. Хсу (Chiou-Ting Hsu) и By (Ja-Ling Wu) [21] был предложен алгоритм встраивания цифрового водяного знака в массив коэффициентов ДКП блоков изображения-контейнера. Приведем основные положения, заложенные авторами в основ) алгоритма.

ПустьС – полутоновое изображение размером Х х У, a W – ЦВЗ, который представляет собой двоичное изображение размером A x Z. ВЦВЗ пиксель может принимать значение или «1», или «0». Разумеется, что непосредственное наблюдение такого изображения невозможно, поскольку интенсивности 0 и 1 отвечают черному цвету (последняя – в некотором приближении). Изображение ЦВЗ можно создать черно-белым, а перед скрытием заменить интенсивность белых пикселей (255) на единицу, например, путем деления всего массива ЦВЗ на 255. При извлечении, наоборот, для визуального наблюдения массив ЦВЗ необходимо умножить на 255.

11.4.2.4 Метод Фридрих.Алгоритм, предложенный Джессикой Фридрих (J. Fridrich) [106]. по сути является комбинацией двух алгоритмов: в соответствии с одним из них скрываемые данные встраиваются в низкочастотные, а с другим – в среднечастотные коэффициенты ДКП. Как было показано автором, каскадное использование двух разных алгоритмов позволяет получить хорошие результаты относительно стойкости стеганографической системы к атакам.