Пропускная способность непрерывного канала связи с помехами

Непрерывным каналом связи будем называть канал, по которому передаются непрерывные сообщения. Пропускную способность непрерывного канала определим, как и в случае дискретного канала, через максимальное среднее количество информации, передаваемой по каналу в единицу времени.

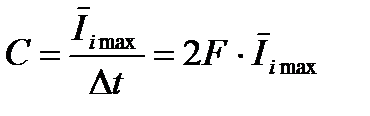, (3.18)

где Dt - временной интервал между дискретами сообщения; F- максимальная частота в спектре входного сообщения, кото­рая соответствует полосе пропускания канала; 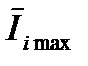- максимальное количество информации, в среднем переда­ваемое одним дискретом сообщения.

Если полагать, что полоса пропускания канала F задана, то определение С сведётся к нахождению 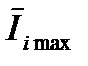. Пусть на входе линии связи канала действует сумма сигнала S(t) и белого шума n(t) со спектральной плотностью N₀

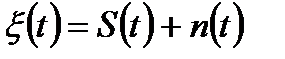, (3.19)

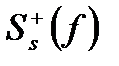где сигнал рассматривается как низкочастотный стационарный слу­чайный процесс, дисперсия которого равна , а спектральная плотность ограничена частотой F. Такое представление соответствует тому, что сигнал и сообщение как процессы совпадают между собой.

Линию связи представим в виде идеального ФНЧ с коэффициентом передачи, равным 1 в полосе F и равным 0 за её пределами. Тогда процесс на выходе линии связи запишется в вид

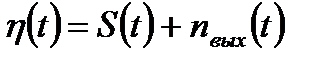, (3.20)

где дисперсия суммарного процесса будет равна

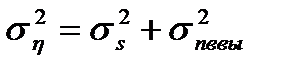. (3.21)

Равенство (3.21) соответствует тому, что процессы S(t) и n_вых(t) являются независимыми. При этом в силу идеальности ФНЧ дисперсия сигнала на выхода ивходе линии связи будет одна и та же, а дисперсия n_вых(t) будет равна

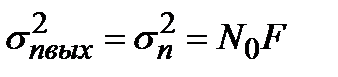. (3.22)

Найдем пропускную способность непрерывного канала связи в предположении, что 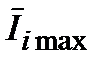, в формуле (3.18) будем искать, накладывая ограничение на 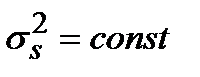. Это означает, что максимальное количество информации будет иметь место, если передаётся гауссовское сообщение. Максимально вредное действие помехи при заданной s² будет также тогда, когда n_вых(t) распределена по гауссовскому закону.

При сделанных допущениях формула (3.8) с учетом (3.15), (3.21) примет вид

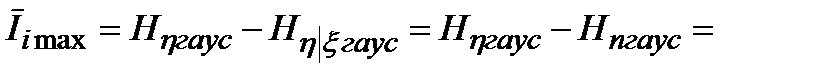
. (3.23)

Подставив (3.23) в выражение (3.18) с учетом (3.22), получим

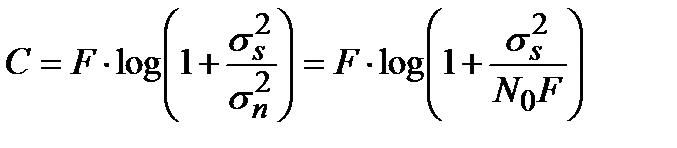. (3.24)

Формула (3.24) определяет пропускную способность непрерывно­го канала связи в зависимости от полосы пропускания линии связи F, мощности сигнала 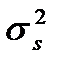и спектральной плотности шума N₀. на входе линии связи. Выражение (3.24) называется формулой Шеннона. Фор­мула Шеннона носит фундаментальный характер в том смысле, что по­казывает принципиальную роль шума как ограничителя пропускной способности.

Рассмотрим зависимость С от F при 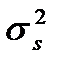= const и N₀ = const

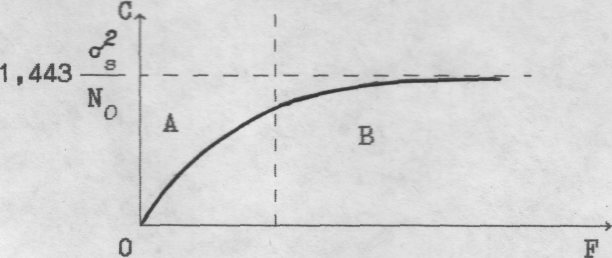
Для пояснения хода графика на рис. найдем значение С при F = 0 и F = 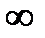. В первом случае имеет место выполнение неравенства 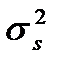/N₀F >> 1, поэтому (3.24) можно записать в виде

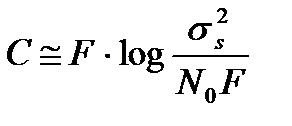. (3.25)

Непосредственная подстановка F = 0 в формулу (3.25) даёт неопределённость типа " 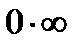" Раскроем её, применив правило Лопиталя.

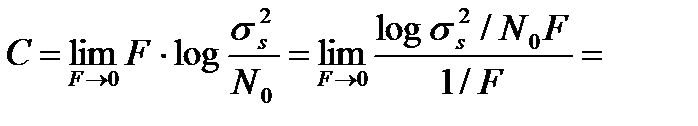
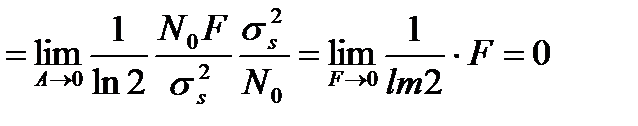. (3.26)

Во втором случае непосредственная подстановка F = ¥ в формулу (3.24) дает неопределённость типа " 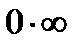". Раскроем её, применив правило Лопиталя.

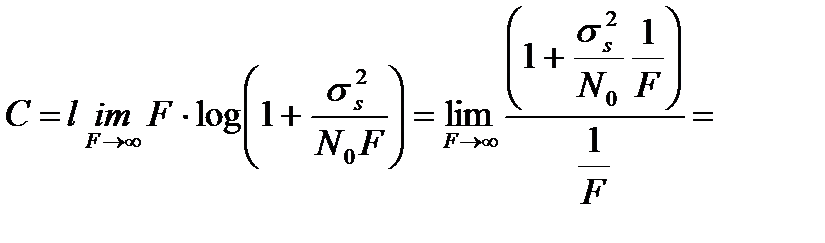
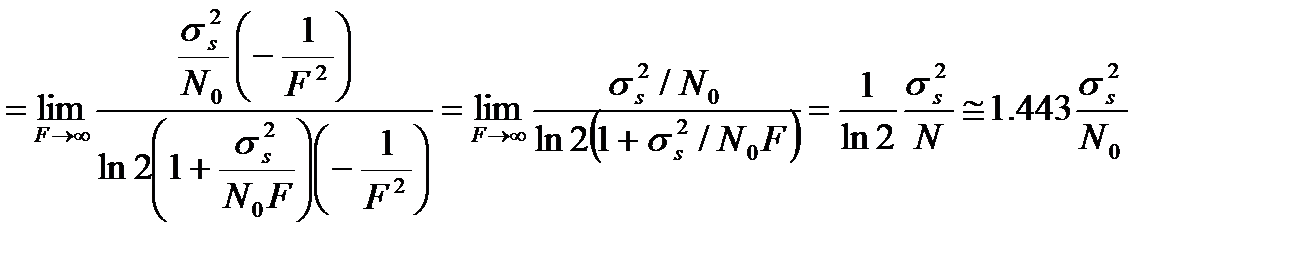. (3.27)

Из графика следует, что при малых F, область А, увеличение полосы пропускания F существенно увеличивает пропуск­ную способность С. При больших F, область В, увеличение F слабо сказывается на росте С, так как С стремится к асимптотическому уровню, который параллелен оси F. Это означает, что при больших F для увеличения С надо илиувеличивать мощность сигнала 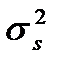, или снижать спектральную плотность шума N₀, то есть следует увеличивать асимптотический уровень.